Элементы теории поля

Проинтерпритируем формулы для криволинейных и поверхностных интегралов физически.

Опред. Если с каждой точкой некоторой пространственной области связана некоторая скалярная или векторная величина, то говорят, что в этой области определено скалярное или векторное поле.

Примером скалярного поля явл., например, поле температур.

Если при этом в пространстве задана нек. система координат, то скалярное поле может быть задано функцией 3-х переменных u = u (x, y, z).

Примером векторного поля является силовое поле (поле сил).

Для задания векторного поля надо задать упорядоченную тройку функций P (x,y,z),

Q (x,y,z), R (x,y,z). Тогда само векторное поле .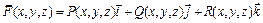

Опред. Пусть u (x, y, z) – некоторое скалярное поле, определённое в некоторой области 3-х мерного пространства. Тогда вектор-функция 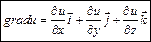называется градиентом скалярного поля u.

Т. о. всякое скалярное поле, если оно задаётся функцией, обладающей тремя частными производными первого порядка всегда порождает векторное поле градиента этого скалярного поля.

Рассмотрим набла-оператор (оператор Гамильтона): .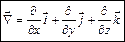

Тогда иначе градиент можно записать так 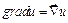(справа- произведение вектора 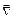на скаляр u.

Градиент скалярного поля u показывает направление наибольшего роста функции u = u (x, y, z).

Величиной градиента наз. скалярное поле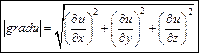

Опред. Рассмотрим векторное поле 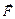и ориентированную поверхность (S). Потоком векторного поля 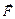через поверхность (S) за единицу времени будем называть след. величину 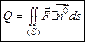или 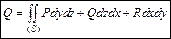. Иначе говоря, поверхностным интегралом 2 рода выражается поток векторного поля через повехность (S) за единицу времени.

Опред. Всякое векторное поле 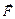порожает скалярное поле 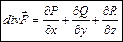, называемое дивергенцией (расходимостью) векторного поля 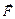. Понятие дивергенции характеризует плотность источников поля в единице объёма.

С помощью дивергенции формула Остроградского- Гаусса примет вид:

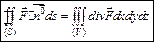
Перейдём к криволинейным интегралам. Криволинейный интеграл 2 рода 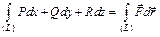представляет себе работу, выполняемую силами поля 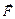по перемещению материальной точки единичной массы вдоль кривой L.

Опред. Интеграл по замкнутому контуру 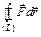равен работе по перемещению мат. точки по замкнутой кривой и наз. циркуляцией поля 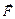вдоль замкнутой кривой L:

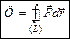
Опред. Ротором (вихрем) векторного порля 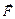наз след. вектор:

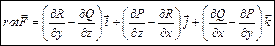
Тогда формула Стокса принимает вид 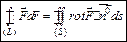. Она связывает циркуляцию поля 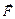с потоком ротора этого поля через поверхность (S).

Градиент, ротор и дивергенцию удобно представлять с помощью оператора Гамильтона .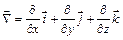

Рассмотрим правила дёйствий с этим вектором:

1. Произведение набла-вектора 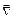на скалярную функцию u (x, y, z) даёт градиент этой функции.

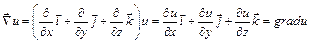
2.Скалярное произведение набла-вектора 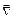на векторную функцию 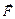даёт дивергенцию этой функции:

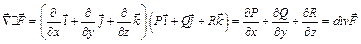
3. Векторное произведение набла-вектора 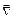на векторную функцию 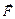даёт ротор этой функции:

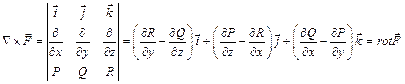
Действия взятия градиента, дивергенции и ротора – векторные дифференциальные операции первого порядка.

Можно также рассмотреть дифференциальные операции 2-го порядка. Среди них важное значение имеет операция взятия дивергенции от градиента:

Пусть имеется скалярное поле u = u (x, y, z) Тогда 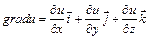. Найдём далее 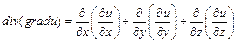, т. е. .

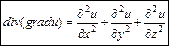Правая часть этого равенства обозначается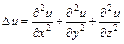

Символ 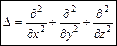называется оператором Лапласа.

При рассмотрении многих задач физики возникает уравнение вида 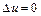, которое называется уравнением Лапласа. А функция, удовлетворяющая этому уравнению, наз. гармонической.