Пусть функция f (t) определена и непрерывна на некотором промежутке, содержащем точку a. Тогда каждому числу x из этого промежутка можно поставить в соответствие число 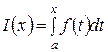 ,
,
определив тем самым на промежутке функцию I (x), которая называется определенным интегралом с переменным верхним пределом. Отметим, что в точке x = a эта функция равна нулю. Вычислим производную этой функции в точке x. Для этого сначала рассмотрим приращение функции в точке x при приращении аргумента D x:
D I (x) = I (x + D x) – I (x) = 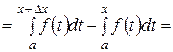
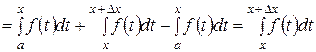 .
.
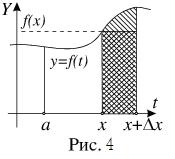
Как показано на Рис. 4, величина последнего интеграла в формуле для приращения D I (x) равна площади криволинейной трапеции, отмеченной штриховкой. При малых величинах D x (здесь, так же как и везде в этом курсе, говоря о малых величинах приращений аргумента или функции, имеем в виду абсолютные величины приращений, так как сами приращения могут быть и положительными, и отрицательными) эта площадь оказывается приблизительно равной площади прямоугольника, отмеченного на рисунке двойной штриховкой. Площадь прямоугольника определяется формулой f (x)D x. Отсюда получаем соотношение
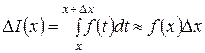 .
.
В последнем приближенном равенстве точность приближения тем выше, чем меньше величина D x.
Из сказанного следует формула для производной функции I (x):
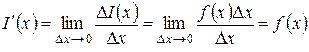 .
.
Производная определенного интеграла по верхнему пределу в точке x равна значению подынтегральной функции в точке x. Отсюда следует, что функция 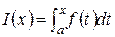 является первообразной для функции f (x), причем такой первообразной, которая принимает в точке x = a значение, равное нулю. Этот факт дает возможность представить определенный интеграл в виде
является первообразной для функции f (x), причем такой первообразной, которая принимает в точке x = a значение, равное нулю. Этот факт дает возможность представить определенный интеграл в виде
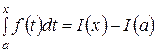 . (1)
. (1)
Пусть F (x) тоже является первообразной для функции f (x), тогда по теореме об общем виде всех первообразных функции I (x) = F (x) + C, где C — некоторое число. При этом правая часть формулы (1) принимает вид
I (x) – I (a) = F (x) + C – (F (a) + C) = F (x) – F (a). (2)
Из формул (1) и (2) после замены x на b следует формула для вычисления определенного интеграла от функции f (t) по промежутку [ a; b ]:
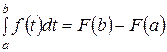 ,
,
которая называется формулойНьютона-Лейбница. Здесь F (x) — любая первообразная функции f (x).
Для того, чтобы вычислить определенный интеграл от функции f (x) по промежутку [ a; b ], нужно найти какую-либо первообразную F (x) функции f (x) и подсчитать разность значений первообразной в точках b и a. Разность этих значений первообразной принято обозначать символом 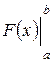 , т.е.
, т.е. 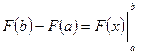 .
.
Замена переменной в определенном интеграле. При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.
ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t 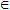 [α,β].
[α,β].
Тогда справедливо следующее равенство:
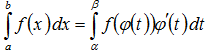
Эта формула носит название формулы замены переменной в определенном интеграле.
Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).
Пример 19. Вычислить 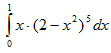
Положим t=2-х2. Тогда dt=d(2-х2)=(2-х2)'dx=-2xdx и xdx=- 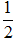 dt. Если х=0, то t=2-02=2, и если х=1, то t=2-12=1. Следовательно:
dt. Если х=0, то t=2-02=2, и если х=1, то t=2-12=1. Следовательно:
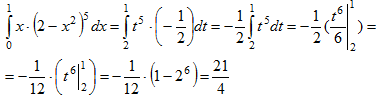
Интегрирование по частям. Метод интегрирования по частям позволяет свести исходный неопределенный интеграл к более простому виду либо к табличному интегралу. Этот метод наиболее часто применяется, если подынтегральная функция содержит логарифмические, показательные, обратные тригонометрические, тригонометрические функции, а также их комбинации.
Формула интегрирования по частям следующая 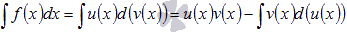 .
.
То есть, подынтегральное выражение f(x)dx представляем в виде произведения функции u(x) на d(v(x)) - дифференциал функции v(x). Далее находим функцию v(x) (чаще всего методом непосредственного интегрирования) и d(u(x)) - дифференциал функции u(x). Подставляем найденные выражения в формулу интегрирования по частям и исходный неопределенный интеграл сводится к разности 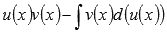 . Последний неопределенный интеграл может быть взят с использованием любого метода интегрирования, в том числе и метода интегрирования по частям.
. Последний неопределенный интеграл может быть взят с использованием любого метода интегрирования, в том числе и метода интегрирования по частям.
В качестве примера найдем множество первообразных функции логарифма.
Пример.
Найти неопределенный интеграл 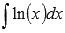
Решение.
Найдем этот неопределенный интеграл методом интегрирования по частям. В качестве функции u(x) возьмем ln(x), а в качестве d(v(x)) оставшуюся часть подынтегрального выражения, то есть dx.
Имеем, 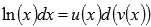 , где
, где 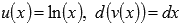 .
.
Дифференциал функции u(x) есть 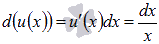 , а функция v(x) – это
, а функция v(x) – это 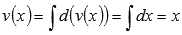 .
.
ЗАМЕЧАНИЕ: константу С при нахождении функции v(x) считают равной нулю.
Теперь все подставляем в формулу интегрирования по частям:
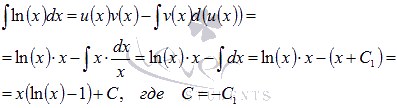
Ответ:
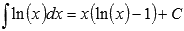 .
.
Самое сложное, что есть в этом методе – это правильно определить, какую часть подынтегрального выражения брать за u(x), а какую за d(v(x)).
Рассмотрим стандартные случаи.
Для интегралов вида 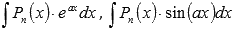 или
или  , где
, где 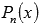 - многочлен степени n, a – коэффициент, в качестве функции u(x) выбираем многочлен
- многочлен степени n, a – коэффициент, в качестве функции u(x) выбираем многочлен 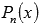 .
.
 2015-06-04
2015-06-04 4168
4168