Интеграл Римана.Определение интеграла Римана

Вопрос 9.Интеграл Римана,свойства.

Пусть 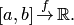Сумма 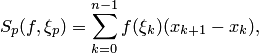где называется интегральной суммой Римана. При этом множество точек 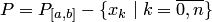разбиением сегмента 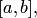а множество 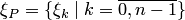— совокупностью промежуточных точек. Обозначим через 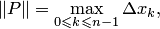где 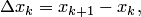норму (или диаметр) разбиения .

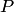Сама функция 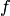при этом называется интегрируемой по Риману на сегменте 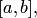а класс всех таких функций будем обозначать символом 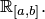Очевидно, что если 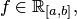то она ограничена на этом сегменте.

Классы интегрируемых функций. Любая функция, ограниченная и непрерывная в некотором промежутке, является интегрируемой на этом промежутке. К классу интегрируемых функций относятся также функции, ограниченные на промежутке интегрирования и имеющие на этом промежутке конечное число точек разрыва первого рода.

Если функция f (x) интегрируема на промежутке [ a, b ], то и функция c f (x), где c – константа, интегрируема на этом промежутке.

Если функция f (x) интегрируема на промежутке [ a, b ], то и функция | f (x) | интегрируема на этом промежутке.

Если функции f (x) и g (x) интегрируемы на промежутке [ a, b ], то и их сумма, разность и произведение интегрируемы на этом промежутке.

Если функция f (x) интегрируема на промежутке [ a, b ], то она интегрируема и в любой части этого промежутка.

Если функция f (x) интегрируема в каждой части некоторого промежутка, то она интегрируема и на всем промежутке.

Если значения интегрируемой функции изменить в конечном числе точек на конечные величины, то интегрируемость функции не нарушится.
Применительно к функции f (x), которая не определена в конечном числе точек промежутка [ a, b ], это означает, что ни существование интеграла 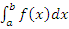, ни его величина не зависят от значений, приписанных функции f (x) в точках ее разрыва.