1. Отрицание. Отрицанием называется новое высказывание, которое истинно, если исходное высказывание ложно и ложное, если исходное – истинно. Отрицание обозначается 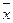 , читается как «не х»
, читается как «не х»
| х | 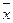
|
.Таблицы такого вида называются таблицами истинности.
2. Дизъюнкция (логическое сложение). Дизъюнкцией двух высказываний x и y называется новое высказывание, которое ложно, если x и y ложное и истинно в остальных случаях, читается «x или y», обозначается 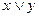 :
:
| х | y | 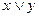
|
3. Коньюнкция (логическое умножение). Конъюнкцией двух высказываний x и y называется новое высказывание, которое истинно, если x и y истинно и ложно в остальных случаях, читается «x и y», обозначается 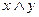 :
:
| х | y | 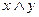
|
4. Импликация. Импликацией двух высказываний x и y называется новое высказывание, которое ложно, если x истинно, а,y ложно и истинно в остальных случаях, читается «если x, то y», обозначается 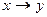 :
:
| х | y | 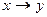
|
5. Эквивалентность. Эквивалентностью двух высказываний x и y называется новое высказывание, которое истинно на одинаковых наборах x и y, читается «x тогда, и только тогда, когда y», обозначается 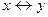 :
:
| х | y | 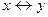
|
6. Сложение по модулю «2». Называется новое высказывание, которое ложно на одинаковых наборах x и y, и истинно в остальных случаях, обозначается 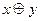 :
:
| х | y | 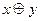
|
7. Стрелка Пирса (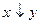 )
)
| х | y | 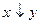
|
8. Штрих Шеффера (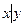 )
)
| х | y | 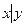
|
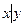
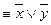 ,
, 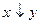
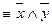
 2015-06-04
2015-06-04 364
364








