При изучении многих явлений приходится встречаться с функциями двух и более независимых переменных. Приведем несколько примеров.
Пример. Площадь 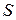 прямоугольника со сторонами, длины которых равны
прямоугольника со сторонами, длины которых равны 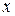 и
и 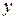 , выражается формулой
, выражается формулой
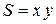 .
.
Каждой паре значений 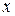 и
и 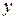 соответствует определенное значение площади
соответствует определенное значение площади 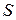 .
. 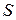 есть функция двух переменных.
есть функция двух переменных.
Пример. Объем 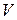 прямоугольного параллелепипеда с ребрами, длины которых равны
прямоугольного параллелепипеда с ребрами, длины которых равны 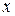 ,
, 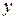 ,
, 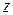 , выражается формулой
, выражается формулой
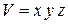 .
.
Здесь 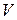 есть функция трех переменных
есть функция трех переменных 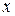 ,
, 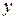 ,
, 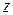 .
.
Пример. 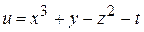
Здесь 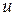 есть функция четырех переменных
есть функция четырех переменных 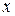 ,
, 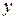 ,
, 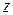 ,
, 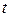 .
.
Определение. Множество всех упорядоченных наборов 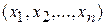 действительных чисел
действительных чисел 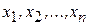 называется
называется 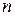 -мерным арифметическим пространством и обозначается Rn, а его элементы – точками пространства Rn (
-мерным арифметическим пространством и обозначается Rn, а его элементы – точками пространства Rn (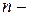 мерными точками). Числа
мерными точками). Числа 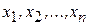 при этом называют координатами точки
при этом называют координатами точки 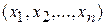 . Точку
. Точку 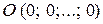 называют началом координат.
называют началом координат.
Пусть DÌ Rn — произвольное множество точек n-мерного арифметического пространства.
Определение. Числовой функцией(или отображением) 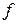 от
от 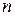 переменных, определенной на множестве D называется закон, по которому каждой точке
переменных, определенной на множестве D называется закон, по которому каждой точке 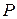
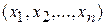 Î D ставится в соответствие некоторое вполне определенное действительное число
Î D ставится в соответствие некоторое вполне определенное действительное число 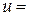
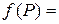
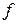
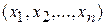 .
.
Обозначения: 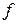 : Rn®R или
: Rn®R или 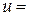
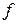
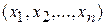 .
.
Множество D при этом называют областью определения, а множество
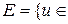 R |
R | 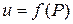 ,
, 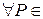 D}— множеством значений функции
D}— множеством значений функции 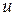 =
= 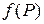 .
.
В частном случае при 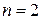 функцию двух переменных можно рассматривать как функцию точек плоскости.
функцию двух переменных можно рассматривать как функцию точек плоскости.
Частное значение функции 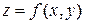 при
при 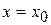 ,
, 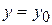 обозначают
обозначают 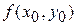 ,
, 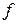
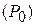 , и т.д.
, и т.д.
Функция двух переменных 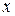 и
и 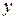 может быть задана аналитическим, табличным, графическим, программным (алгоритмом вычисления
может быть задана аналитическим, табличным, графическим, программным (алгоритмом вычисления 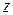 по значениям
по значениям 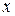 и
и 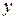 ) и другими способами.
) и другими способами.
Функцию двух переменных 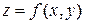 можно изобразить в трехмерном пространстве при выбранной декартовой системе координат
можно изобразить в трехмерном пространстве при выбранной декартовой системе координат 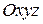 как множество точек пространства
как множество точек пространства 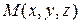 ÎR3, координаты которых удовлетворяют уравнению
ÎR3, координаты которых удовлетворяют уравнению 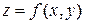 , которое, вообще говоря, есть уравнение некоторой поверхности в R3. Проекцией этой поверхности на плоскость
, которое, вообще говоря, есть уравнение некоторой поверхности в R3. Проекцией этой поверхности на плоскость 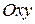 является область определения D
является область определения D 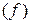 . Каждый перпендикуляр к плоскости
. Каждый перпендикуляр к плоскости 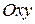 пересекает поверхность
пересекает поверхность 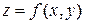 не более чем в одной точке (в силу однозначности функции).
не более чем в одной точке (в силу однозначности функции).
Замечание. Функцию трех и более переменных изобразить графически невозможно.
Пример. Найти область определения функции 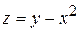 .
.
Решение. Аналитическое выражение 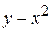 имеет смысл при любых действительных значениях
имеет смысл при любых действительных значениях 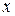 и
и 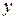 . Следовательно, областью определения является вся числовая плоскость
. Следовательно, областью определения является вся числовая плоскость 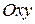 т.е. D
т.е. D  = R2.
= R2.
Пример. Найти область определения функции 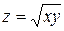 .
.
Решение. Аналитическое выражение 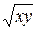 имеет смысл при
имеет смысл при 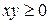 , следовательно, областью определения этой функции являются I и III четверти плоскости
, следовательно, областью определения этой функции являются I и III четверти плоскости 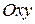 , включая оси
, включая оси 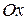 и
и 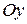 , т.е. область, заштрихованная на рисунке.
, т.е. область, заштрихованная на рисунке. 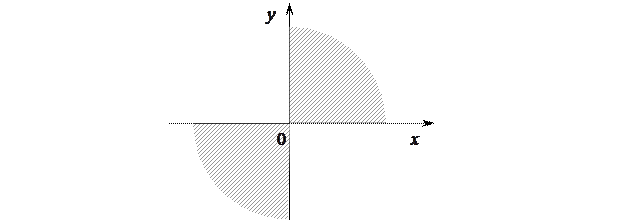
Пример. Найти область определения функции 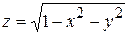 .
.
Решение. Для того, чтобы 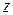 имело действительное значение, необходимо, чтобы под корнем было неотрицательное число, т.е.
имело действительное значение, необходимо, чтобы под корнем было неотрицательное число, т.е. 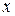 и
и 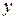 должны удовлетворять неравенству
должны удовлетворять неравенству 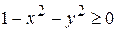 или
или 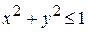 .
.
Все точки 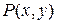 , координаты которых удовлетворяют указанному неравенству, лежат в круге радиуса 1 с центром в начале координат и на границе этого круга, т.е. область, заштрихованная на рисунке.
, координаты которых удовлетворяют указанному неравенству, лежат в круге радиуса 1 с центром в начале координат и на границе этого круга, т.е. область, заштрихованная на рисунке. 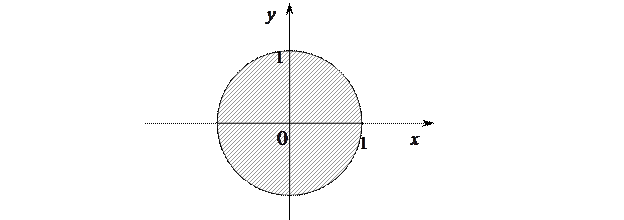
Пример. Найти область определения, множество значений функции 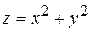 , построить график.
, построить график.
Решение. Область определения этой функции D 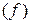 = R2, множество значенийЕ
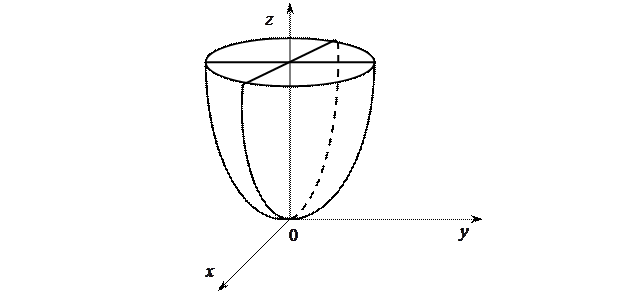
= R2, множество значенийЕ 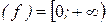 . Графиком данной функции в пространстве R3 является параболоид вращения.
. Графиком данной функции в пространстве R3 является параболоид вращения.
Пример. Найти область определения и множество значений функции 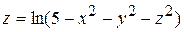 .
.
Решение. Данная функция определена, если 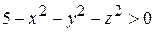 или
или 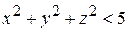 , откуда D
, откуда D 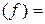 {
{ 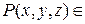 R3 |
R3 | 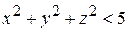 }, т. е. областью определения D
}, т. е. областью определения D 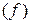 данной функции является множество точек открытого трёхмерного шара радиуса
данной функции является множество точек открытого трёхмерного шара радиуса 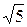 , а Е(
, а Е(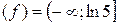 .
.
 2015-06-04
2015-06-04 331
331








