2015-06-04
607
В результате исследования объективно существующих связей между явлениями вскрываются причинно-следственные отношения, что позволяет выявлять факторы, оказывающие основное влияние на вариацию изучаемых явлений и процессов.
Признаки, обусловливающие изменения других, связанных с ними признаков, называются факторными. Признаки, изменяющиеся под действием факторных признаков, являются результативными. Связи между явлениями и их признаками классифицируются по степени тесноты связи, направлению и аналитическому выражению.
Парная корреляция – связь между двумя признаками (результативным и факторным).
Частная корреляция – зависимость между результативным и одним из факторных признаков при фиксированном значении других факторных признаков.
Множественная корреляция – зависимость результативного и двух и более факторных признаков, включенных в исследование.
Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной корреляции) и между результативным и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции.
Регрессионный анализ заключается в определении аналитического выражении связи.
Регрессия может быть однофакторной (парной) и многофакторной (множественной).
По форме зависимости различают:
а) линейную регрессию, которая выражается уравнением прямой вида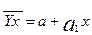 
; где
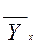- среднее значение результативного признака, изменяющееся в соответствии с величиной факторного признака;
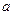- свободный член уравнения, выражающий среднее значение результативного признака, которое возникает при отсутствии влияния факторного изучаемого признака;
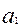- коэффициент связи, показывающий изменение величины результативного признака при изменении факторного на 1.
б) нелинейную регрессию, которая рассчитывается уравнением вида:
- парабола: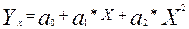 
;
- гипербола: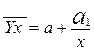 
.
Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов.
В случае прямолинейной связи между X и Y вида 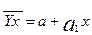параметры уравнения a и 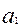отыскиваются путем решения системы нормальных уравнений:
.
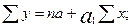
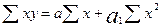Для нахождения параметров а и b при линейной зависимости можно использовать готовые формулы:
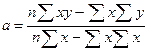(75); 
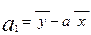(76).
Уравнение гиперболы используется при обратной зависимости между двумя величинами (с уменьшением Х увеличивается Y, и наоборот, с увеличением Х уменьшается Y)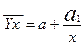 
.
Система нормальных уравнений для нахождения параметров гиперболы а и b имеет вид: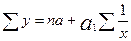 
;
.
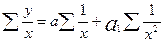Формула коэффициента корреляции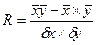 
; (77) где: 
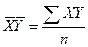(78); 
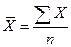(79); 
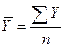(80); δх 
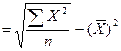(81); δу 
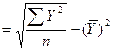(82).
Положительное значение коэффициента корреляции свидетельствует о наличии прямой зависимости между признаками, а отрицательное – об обратной зависимости.
Величина коэффициента корреляции может изменяться от (-1) до 0 и от 0 до (+1). Чем ближе коэффициент корреляции к (+1) или (-1), тем более тесной, более близкой к средней является зависимость.
Коэффициент детерминации определяется по формуле:
d = R2 (83)
Коэффициент детерминации показывает, на сколько процентов результативный признак зависит от факторного.
