Виды степенных средних

Вид степенной средней	Показатель степени (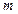)	Формула расчета
простая	взвешенная
гармоническая	- 1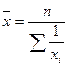
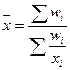
геометрическая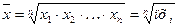
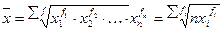
арифметическая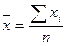
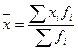
квадратическая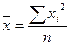
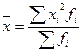
кубическая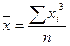

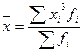
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени k увеличивается и соответствующая средняя величина:

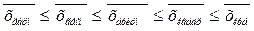, (2.17)

В статистической практике чаще, чем остальные виды средних взвешенных, используется средняя арифметическая и средняя гармоническая взвешенные. Выбор вида степенной средней определяется экономическим содержанием задачи и наличием данных.

Рассмотрим среднюю арифметическую простую и взвешенную.

Пример: Студент Петров по результатам учебного семестра имеет следую­щие оценки: теория бухгалтерского учета - 4, экономическая ста­тистика - 5, финансы, денежное обращение и кредит - 3, эконо­мика фирмы - 2. Какова его средняя оценка по результатам семестра?

Поскольку каждая оценка встречается один раз, для расчета средней применяем формулу арифметической простой:

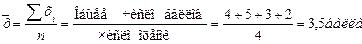
Перечисленные дисциплины студент Петров сдал в среднем на 3,5 балла.

Пример: Имеются следующие данные о распределении бригад по уровню выработки продукции (табл. 2.10).

Таблица 2.10