2015-06-04
2420
Интегрирование иррациональных и тригонометрических функций
Методом замены переменной интегралы от рациональных функций можно привести интегралы вида:
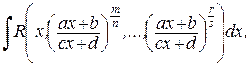
где символ R означает, что над аргументами такой функции производятся рациональные операции. Если в интегралах такого вида сделать подстановку:
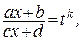где
k = HOK (n,..., s) - наименьшее общее кратное “показателей корней”, то ясно, что все аргументы функции R, а также dx можно выразить, используя только целые степени переменной t. Это означает, что подынтегральная функция примет вид рациональной дроби.
Пример. Привести к рациональному интеграл:
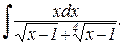
Используем подстановку: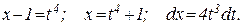 
Подставляя в исходный интеграл, получаем:
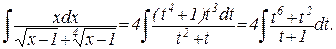
(Далее нужно выделить целую часть и проинтегрировать полученную сумму).
Пример. Привести к рациональному интеграл:
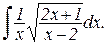
Используем подстановку: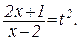 
Выразим отсюда х:
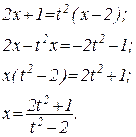
Продифференцировав это выражение, найдем dx:
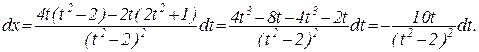
Подставляя в исходный интеграл, получим:
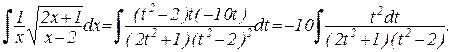
(Далее надо использовать алгоритм интегрирования рациональной функции).
