Интегрирование выражений, содержащих радикалы из квадратичных функций

В качестве общей рекомендации при интегрировании выражений, содержащий квадратный трехчлен ax² + bx + c, можно указать на целесообразность применения к нему преобразования, известного из школьного курса математики как “выделение полного квадрата”, например:

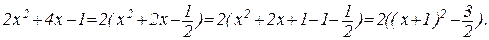
Это означает, например, что интегралы вида

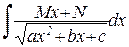
с помощью простейших преобразования и замены переменных можно привести к одному из простейших двух типов:

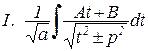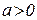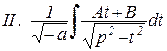, при . при .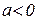

Разделив затем почленно подынтегральные выражения, получим два табличных интеграла. Заметим, что в некоторых случаях “избавиться от иррациональности” помогают так называемые тригонометрические подстановки:

а) если подынтегральная функция содержит выражение вида ,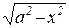

можно использовать замены: x = a·cost или x = a·sint;

б) для интегралов, содержащих выражение 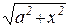, можно использовать подстановки:

x = a·tgt или x = a·ctgt;

в) если под знаком интеграла есть выражения 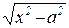, можно сделать замены:

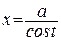или 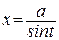и т.д.

Пример. Вычислить интеграл

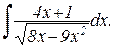
Выделяем полный квадрат:

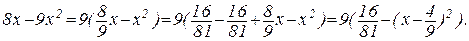
Сделаем подстановку: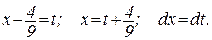

Подставляя в исходный интеграл, получим:

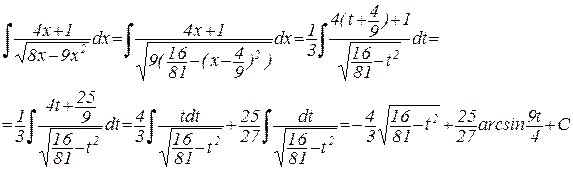
(возвращаемся к “старой переменной”)

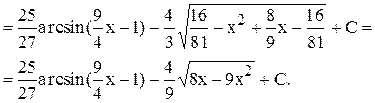
Пример. Вычислить интеграл: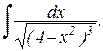

Применяем одну из тригонометрических подстановок: x = 2sint; dx = 2costdt.

Подставив в исходный интеграл, получаем:

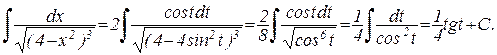
Сделав “обратную замену”, получим: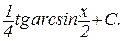

Итак, основным методом интегрирования простейших иррациональных функций является метод замены переменной.

2. Интегрирование выражений, содержащих
тригонометрические функции

а) Интегралы вида: 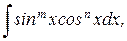где m, n - целые числа.

Интегрирование таких выражений сводится к нескольким случаям.

I. Если m и n - четные положительные числа, то можно “понизить степень”, используя известные формулы тригонометрии:

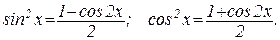
Пример. Вычислить интеграл:

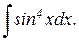
Решение. “Понижаем степень” синусов:

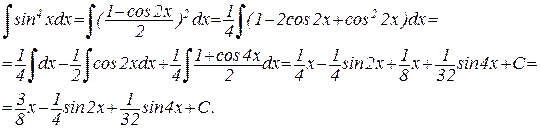
II. Если хотя бы одно из чисел m и n (например, n) положительное нечетное, то можно поступить следующим образом: n = 2k + 1, тогда:

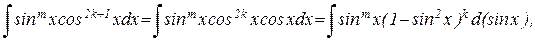
и можно делать подстановку sin x = t.

Ясно, что в случае m = 2k + 1 подынтегральное выражение можно привести к виду, позволяющему сделать замену cosx = t.

Пример.

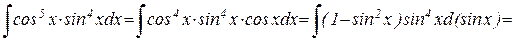
{замена sin x = t }

Заметим, что такие способы применимы и в случаях, если подынтегральная функция имеет вид R(sinx; cosx) и нечетна относительно одного из своих аргументов sin x или cos x. Если же функция R(sinx; cosx) не изменяется при одновременной замене sin x на (-sin x) и cos x на (-cos x), то можно применить подстановку tg x = t.

Пример. Вычислить интеграл:

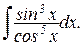
1) sin x - в нечетной степени, поэтому подынтегральное выражение можно “выразить через косинус”:

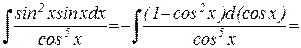{замена cos x = t }

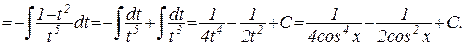
2) cos x - в нечетной степени, значит можно поступить следующим образом:

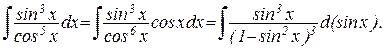
3) При замене sin x на (-sin x) и cos x на (-cos x) подынтегральная функция не изменяется:

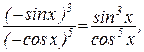
поэтому можно сделать замену tgx = t, тогда по известным формулам тригонометрии:

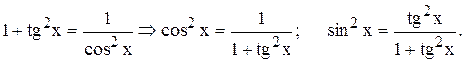
Отсюда получаем:

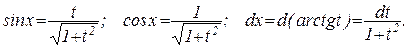
Подставляя в исходный интеграл, получим:

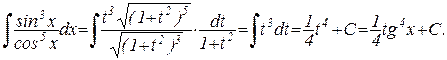
б) Интегралы вида: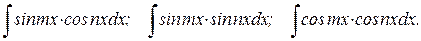

При вычислении таких интегралов можно использовать формулы преобразования произведений тригонометрических функций в суммы:

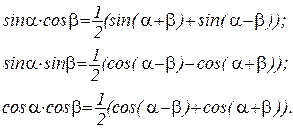
Например:

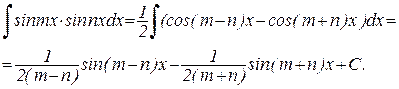
Таким образом, интегрирование тригонометрических функций осуществляется методом непосредственного интегрирования или подставок.