Сходимоть порядка k

Если, сверх того, выполнено неравенство 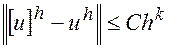, где 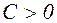, 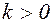– некоторые постоянные, не зависящие от 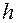, то будем говорить, что имеет место сходимость порядка 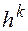или, что разностная схема имеет 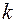- й порядок точности. как правило, систему

Аппроксимация

Не всегда (2) удается выбрать так, чтобы 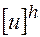в точности ей удовлетворяла. При подстановке в уравнение (8.2) возникает некоторая невязка:

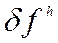- невязка

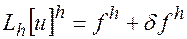(3)

Определение 8.2

Будем говорить, что разностная схема (8.2) аппроксимирует исходную дифференциальную задачу (8.1) на решении 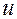, если

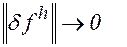при 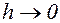, т.е. норма невязки стремится к нулю при стремлении к нулю шага разностной сетки.