ОБЩИЕ ПОНЯТИЯ РЕЗНОСТНЫХ СХЕМ.
Пусть в некоторой области D поставлена некоторая дифференциальная краевая задача
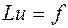 , (1)
, (1)
где через 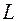 обозначен некоторый заданный дифференциальный оператор, действующий на искомую функцию
обозначен некоторый заданный дифференциальный оператор, действующий на искомую функцию 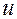 , через
, через 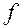 - правая часть. Примем, что оператор
- правая часть. Примем, что оператор 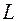 включает как дифференциальное уравнение, так и граничные условия.
включает как дифференциальное уравнение, так и граничные условия.
Обозначим через 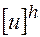 таблицу значений искомого решения
таблицу значений искомого решения 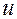 в узлах сетки
в узлах сетки 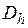 . Тогда соответствующая (8.1) разностная краевая задача (разностная схема) запишется в виде
. Тогда соответствующая (8.1) разностная краевая задача (разностная схема) запишется в виде
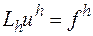 . (2)
. (2)
Сходимость
Будем говорить, что решение 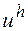 разностной краевой задачи (8.2) при сгущении сетки сходится к решению
разностной краевой задачи (8.2) при сгущении сетки сходится к решению 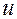 дифференциальной краевой задачи (8.1), если
дифференциальной краевой задачи (8.1), если
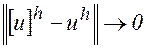
 2015-06-05
2015-06-05 231
231







