Сходимость порядка k

Если, сверх того, имеет место неравенство ,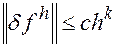

где 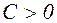, 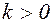– некоторые постоянные, не зависящие от 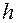, то будем говорить, что имеет место аппроксимация порядка 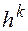или порядка 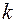относительно величины .

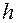Устойчивость

Будем называть разностную схему (2) устойчивой, если существуют такие постоянные 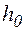и 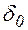, что при любом 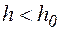и любой сеточной функции 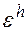, такой, что 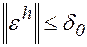разностная задача

,

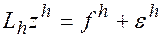полученная из (8.2) добавление к правой части возмущения 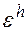имеет место и имеет только одно решение 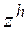, причем справедлива оценка

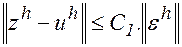, (8.4)

где 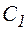– некоторая постоянная, не зависящая от .

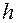Малое возмущение 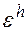правой части разностной схемы (2) вызывает равномерно относительно 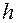малое возмущение 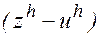решения .

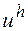3.