Основные понятия теории систем

1. Основное определение понятий «система», «элемент», «подсистема», «цель», «связь».

2. Понятия, которые характеризуют функционирование и развитие системы.

Термин система используют в тех случаях, когда хотят охарактеризовать исследуемый объект как нечто целое, сложное, о котором невозможно сразу дать представление, показать его, изобразив графически или математически. Существует много определений системы. Дадим сначала простое интуитивное определение.

Система - совокупность элементов, находящихся в определённых отношениях между собой и образующих некоторое целостное единство. Или: система - объект, процесс в котором участвующие элементы связаны некоторыми связями (отношениями).

Если хотим подчеркнуть связь системы с внешней средой, то можно дать ещё и такое определение: Система – совокупность элементов, находящихся в определённых отношениях друг с другом и со средой.

Формализованная запись определения системы:

S_def ,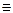

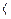
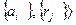где , .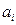

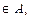
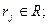
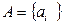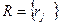Определение системы по М. Месаровичу:

Если 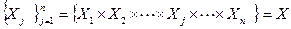- декартово произведение множеств Х_j, то система - это 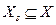или 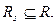, если 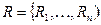- множество отношений.

Если 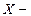входы (воздействующие объекты), 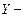выходы (результаты), то 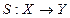или 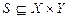, а точнее –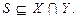

Наконец, к понятию «система» можно относиться как к категории теории отражения, познания:

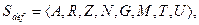
где Z, N, G, M, T, U – параметры совокупности целей системы, субъекта системы, языка субъекта, задач проектирования, эксперимента, управления соответственно.

Выбор определения системы зависит от этапа представления объекта, конкретной ситуации. Например, параметры Z, N, G, M, T, U не всегда следует учитывать. В связи с подвижностью понятия система разработчики вводят «рабочее» определение системы.

Различные концепции иерархии представим в терминах математической теории систем. С этой целью мы формализуем в теоретико-множественных терминах различные понятия систем, подсистем и их взаимозависимостей. Роль математики математической теории в методологии теории систем иллюстрируется на рис. 1.

Математическая концепция общей системы S есть отношение на абстрактных множествах X и Y:

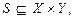
где X – множество входов, Y – множество выходов. Элементы множеств X и Y являются соответственно входами и выходами, поэтому представление системы как отношения является представлением входа – выхода.

Рис. 1. Методология формулировки и анализа проблемы

Если 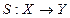, то S является функциональной системой и её входы можно рассматривать как причину и её выходы – как эффект. Следовательно, множества входов и выходов можно отнести соответственно к объектам причины и эффекта. Эта терминология относится к моделированию причинно-следственных (эффектных) явлений.