Двухшаговый метод наименьших квадратов (ДМНК) применяется как к точно идентифицированной, так и к сверхидентифицированной системе.
Применение метода предусматривает следующие шаги:
1. Построение приведенной формы модели (ПФМ).
2. Для каждого уравнения структурной формы модели выполняются следующие действия:
· находят эндогенные переменные, являющиеся факторными признаками (стоят в правой части уравнения);
· для этих переменных определяют их выровненные значения 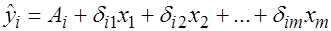 , используя соответствующее уравнение ПФМ;
, используя соответствующее уравнение ПФМ;
· находят параметры рассматриваемого уравнения структурной формы модели обычным МНК, заменяя исходные значения эндогенных переменных-факторов их выровненными значениями.
Сверхидентифицируемая структурная модель может быть двух типов:
1) все уравнения системы сверхидентифицируемы;
2) система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.
Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то вычисление структурных коэффициентов возможно из системы приведенных уравнений.
Пример 5.3.
Имеются квартальные данные об объемах валового внутреннего продукта (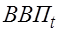 , трлн. руб.), расходов на конечное потребление (
, трлн. руб.), расходов на конечное потребление (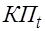 , трлн. руб.), валового накопления (
, трлн. руб.), валового накопления (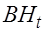 , трлн. руб.) и чистого экспорта (
, трлн. руб.) и чистого экспорта (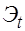 , трлн. руб.).
, трлн. руб.).
Таблица 5.7 Динамика внутреннего валового продукта по кварталам
| Номер наблюдения | Год, квартал | ВВПt | КПt | ВНt | Эt |
| 2003, 1 квартал | 330,10 | 260,15 | 43,40 | 26,55 | |
| 2003, 2 квартал | 341,60 | 248,27 | 73,10 | 20,22 | |
| 2003, 3 квартал | 395,70 | 266,59 | 124,23 | 4,89 | |
| 2003, 4 квартал | 361,10 | 251,42 | 105,49 | 4,19 | |
| 2004, 1 квартал | 322,80 | 257,22 | 55,71 | 9,87 | |
| 2004, 2 квартал | 330,10 | 254,48 | 64,34 | 11,28 | |
| 2004, 3 квартал | 374,00 | 244,54 | 116,24 | 13,22 | |
| 2004, 4 квартал | 350,10 | 240,90 | 86,66 | 22,55 | |
| 2005, 1 квартал | 321,40 | 255,54 | 52,31 | 13,55 | |
| 2005, 2 квартал | 327,30 | 257,72 | 63,56 | 6,01 | |
| 2005, 3 квартал | 384,70 | 266,72 | 112,83 | 5,16 | |
| 2005, 4 квартал | 362,60 | 278,34 | 77,86 | 6,39 | |
| 2006, 1 квартал | 316,70 | 247,37 | 73,12 | -3,79 | |
| 2006, 2 квартал | 324,20 | 237,30 | 87,60 | -0,70 | |
| 2006, 3 квартал | 350,80 | 270,15 | 62,16 | 18,49 | |
| 2006, 4 квартал | 329,70 | 275,55 | -6,67 | 60,82 | |
| 2007, 1 квартал | 310,80 | 244,14 | 23,93 | 42,73 | |
| 2007, 2 квартал | 334,20 | 232,50 | 51,61 | 50,09 | |
| 2007, 3 квартал | 390,90 | 242,69 | 89,33 | 58,87 | |
| 2007, 4 квартал | 369,40 | 244,74 | 41,35 | 83,31 | |
| 2008, 1 квартал | 346,30 | 221,76 | 40,13 | 84,41 | |
| 2008, 2 квартал | 368,40 | 222,53 | 61,49 | 84,38 | |
| 2008, 3 квартал | 432,00 | 253,44 | 99,66 | 78,90 | |
| 2008, 4 квартал | 399,80 | 250,08 | 85,17 | 64,55 | |
| 2009, 1 квартал | 347,10 | 235,57 | 46,33 | 65,21 | |
| 2009, 2 квартал | 364,15 | 242,31 | 70,86 | 50,98 | |
| 2009, 3 квартал | 424,67 | 261,28 | 116,53 | 46,86 | |
| 2009, 4 квартал | 399,80 | 265,24 | 100,71 | 33,85 | |
| 2010, 1 квартал | 363,31 | 271,79 | 53,62 | 37,90 | |
| 2010, 2 квартал | 382,50 | 269,36 | 69,12 | 44,02 | |
| 2010, 3 квартал | 450,21 | 289,35 | 111,53 | 49,33 | |
| 2010, 4 квартал | 417,90 | 287,06 | 87,79 | 43,05 | |
| 2011, 1 квартал | 377,14 | 271,76 | 50,60 | 54,77 | |
| 2011, 2 квартал | 399,38 | 279,64 | 74,57 | 45,17 | |
| 2011, 3 квартал | 470,24 | 295,94 | 127,63 | 46,66 | |
| 2011, 4 квартал | 443,71 | 300,05 | 97,98 | 45,68 | |
| 2012, 1 квартал | 405,83 | 298,01 | 58,24 | 49,58 | |
| 2012, 2 квартал | 431,29 | 296,59 | 80,61 | 54,09 | |
| 2012, 3 квартал | 499,50 | 316,51 | 122,58 | 60,42 | |
| 2012, 4 квартал | 478,06 | 306,31 | 112,89 | 58,86 | |
| 2013, 1 квартал | 435,47 | 314,10 | 60,92 | 60,45 | |
| 2013, 2 квартал | 463,66 | 309,69 | 84,13 | 69,83 | |
| 2013, 3 квартал | 535,01 | 336,24 | 127,61 | 71,15 | |
| 2013, 4 квартал | 510,18 | 318,43 | 128,26 | 63,49 |
На основе данных была построена модель:
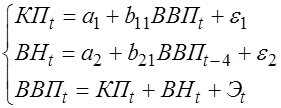 ,
,
где 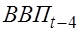 — объем
— объем 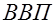 за аналогичный квартал предыдущего года.
за аналогичный квартал предыдущего года.
Выполним проверку системы на идентификацию с помощью необходимого условия.
Для первого уравнения имеем:
· количество эндогенных переменных, входящих в это уравнение, равно двум (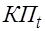 и
и 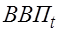 t),
t), 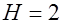 ;
;
· количество предопределенных переменных, не входящих в это уравнение, равно двум (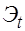 и
и 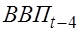 ),
), 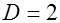 .
.
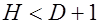 , следовательно, уравнение сверхидентифицировано.
, следовательно, уравнение сверхидентифицировано.
Для второго уравнения имеем:
· количество эндогенных переменных, входящих в это уравнение, – одна (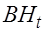 ),
), 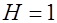 ;
;
· количество предопределенных переменных, не входящих в это уравнение, – одна (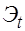 ),
), 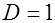
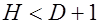 , следовательно, уравнение сверхидентифицировано.
, следовательно, уравнение сверхидентифицировано.
Третье уравнение является тождеством и на идентификацию не проверяется.
Поскольку оба уравнений системы сверхидентифицированы, то и система сверхидентифицирована.
Выполним проверку системы на идентификацию с помощью достаточного условия.
Определим матрицу коэффициентов при переменных, отсутствующих в первом уравнении (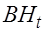 ,
, 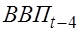 ,
, 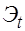 ):
):
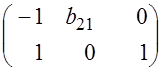 .
.
Определитель данной матрицы не равен нулю, ранг матрицы равен двум, что на единицу меньше количества эндогенных переменных в системе. Таким образом, достаточное условие соблюдается.
Определим матрицу коэффициентов при переменных, отсутствующих во втором уравнении (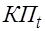 ,
, 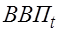 ,
, 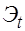 ):
):
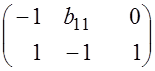 .
.
Ранг данной матрицы равен 2, следовательно, достаточное условие соблюдается.
Обобщая выводы относительно идентификации системы, получаем, что система имеет решение и является сверхидентифицированной.
Для нахождения ее коэффициентов применим двухшаговый метод наименьших квадратов.
1 шаг. Запишем приведенную форму модели:
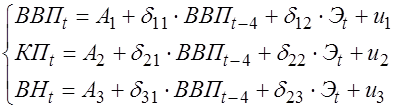 .
.
Вычисление параметров каждого уравнения этой модели с помощью МНК проведем по укороченным рядам: все показатели, кроме 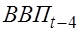 берутся с пятого по 44 наблюдение, а показатель
берутся с пятого по 44 наблюдение, а показатель 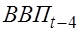 — с первого по 40-е наблюдение (табл.5.7).
— с первого по 40-е наблюдение (табл.5.7).
В результате система уравнений примет вид:
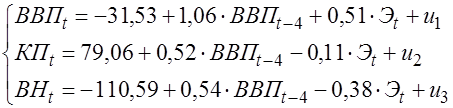 .
.
2 шаг. Рассмотрим уравнения структурной формы модели (СФМ).
В первом уравнении СФМ эндогенной переменной-фактором является переменная 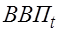 . Найдем ее выровненные значения по первому уравнению ПФМ.
. Найдем ее выровненные значения по первому уравнению ПФМ.
Таблица 5.8 Расчет выровненный значений 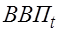
| Номер наблюдения | ВВПt-4 | Эt | Выровненные значения ВВПt |
| 330,10 | 9,87 | ||
| 341,60 | 11,28 | ||
| 395,70 | 13,22 | ||
| 361,10 | 22,55 | ||
| 322,80 | 13,55 | ||
| 330,10 | 6,01 | ||
| 374,00 | 5,16 | ||
| 350,10 | 6,39 | ||
| 321,40 | -3,79 | ||
| 327,30 | -0,70 | ||
| 384,70 | 18,49 | ||
| 362,60 | 60,82 | ||
| 316,70 | 42,73 | ||
| 324,20 | 50,09 | ||
| 350,80 | 58,87 | ||
| 329,70 | 83,31 | ||
| 310,80 | 84,41 | ||
| 334,20 | 84,38 | ||
| 390,90 | 78,90 | ||
| 369,40 | 64,55 | ||
| 346,30 | 65,21 | ||
| 368,40 | 50,98 | ||
| 432,00 | 46,86 | ||
| 399,80 | 33,85 | ||
| 347,10 | 37,90 | ||
| 364,15 | 44,02 | ||
| 424,67 | 49,33 | ||
| 399,80 | 43,05 | ||
| 363,31 | 54,77 | ||
| 382,50 | 45,17 | ||
| 450,21 | 46,66 | ||
| 417,90 | 45,68 | ||
| 377,14 | 49,58 | ||
| 399,38 | 54,09 | ||
| 470,24 | 60,42 | ||
| 443,71 | 58,86 | ||
| 405,83 | 60,45 | ||
| 431,29 | 69,83 | ||
| 499,50 | 71,15 | ||
| 478,06 | 63,49 |
После этого применим к первому уравнению СФМ метод наименьших квадратов, используя в качестве исходной информации значения эндогенной переменной-результата (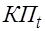 ) и выровненные значения эндогенной переменной фактора (
) и выровненные значения эндогенной переменной фактора (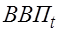 ). В результате получим:
). В результате получим:
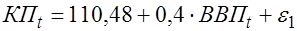
Фактическое значение 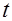 -критерия Стьюдента для коэффициента регрессии в этом уравнении равно 7,95, табличное 2,0244 (
-критерия Стьюдента для коэффициента регрессии в этом уравнении равно 7,95, табличное 2,0244 (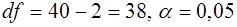 ), следовательно коэффициент при переменной
), следовательно коэффициент при переменной 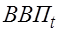 значим. Значимо и уравнение в целом (
значим. Значимо и уравнение в целом (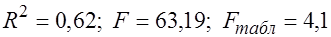 ).
).
Второе уравнение не содержит эндогенный переменных-факторов, поэтому его параметры можно найти, применяя к нему обычный МНК. В результате получим следующее уравнение регрессии:
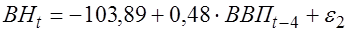
Это уравнение также имеет значимый коэффициент (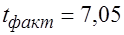 ) и значимо в целом (
) и значимо в целом (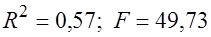 ).
).
Третье уравнение СФМ не является уравнением регрессии и не имеет неизвестных параметров (все параметры равны единице).
Таким образом, получена следующая система уравнений:
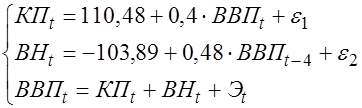 .
.
 2015-06-05
2015-06-05 455
455







