Процедура применения КМНК предполагает выполнение следующих этапов работы.
1. Структурная модель преобразовывается в приведенную форму модели.
2. Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты 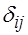 .
.
3. Коэффициенты приведенной формы модели трансформируются в параметры структурной модели.
Пример 5.2.
Исследуется зависимость спроса и предложения некоторого товара от его цены 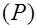 , дохода на душу населения и инвестиций в производство
, дохода на душу населения и инвестиций в производство 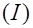 . Модель спроса и предложения имеет вид:
. Модель спроса и предложения имеет вид:
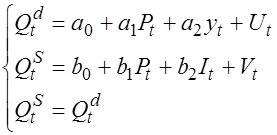 ,
,
где 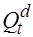 — спрос в момент времени
— спрос в момент времени 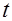 ;
;
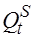 — предложение в момент времени
— предложение в момент времени 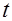 .
.
Учитывая вид третьего уравнения системы, обозначим 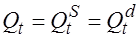 .
.
В данной модели 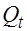 и
и 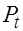 — эндогенные переменные, причем переменная
— эндогенные переменные, причем переменная 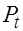 является эндогенной как по экономическому смыслу (цена зависит от спроса и предложения), так и в силу наличия тождества
является эндогенной как по экономическому смыслу (цена зависит от спроса и предложения), так и в силу наличия тождества 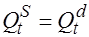 . Переменные
. Переменные 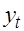 и
и 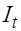 являются экзогенными переменными. Каждое уравнение системы точно идентифицировано. Применим КМНК, используя следующую информацию:
являются экзогенными переменными. Каждое уравнение системы точно идентифицировано. Применим КМНК, используя следующую информацию:
Таблица 5.6
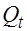
| |||||||||
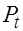
| |||||||||
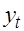
| |||||||||
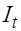
|
Запишем приведенную форму модели:
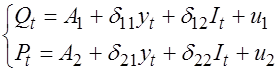
Оценку параметров каждого уравнения приведенной формы модели выполним, используя обычный МНК. В результате получим:
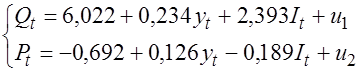
Выполним переход к структурной форме модели. Найдем уравнение спроса.
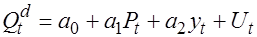
Для этого из второго уравнения приведенной модели выразим 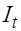 и подставим его в первое уравнение:
и подставим его в первое уравнение:
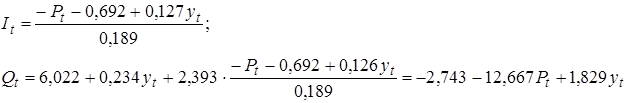
Получили первое уравнение структурной формы модели. Аналогично найдем и второе уравнение структурной формы модели, характеризующее функцию предложения: 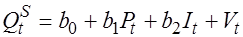 . Для этого из первого уравнения приведенной формы модели исключим
. Для этого из первого уравнения приведенной формы модели исключим 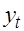 , выразив его через второе уравнение и подставив в первое.
, выразив его через второе уравнение и подставив в первое.
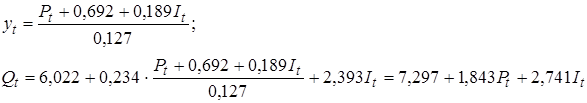
В итоге модель спроса и предложения имеет вид:
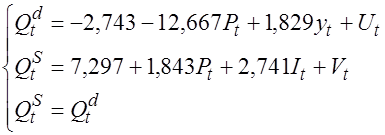
 2015-06-05
2015-06-05 379
379








