Лекция №6
Тема: РАСЧЕТЫ СВОБОДНО ПОДВЕШЕННЫХ ПРОВОДОВ И ПРОСТЫХ КОНТАКТНЫХ ПОДВЕСОК
Уравнение провисания свободно подвешенного провода
Если провод с постоянной площадью сечения подвесить между двумя точками, расположенными на одном уровне, то под действием равномерно распределенной по его длине нагрузки от веса провод примет очертание цепной линии (рис. 6.1). Жесткость проводов и тросов сказывается только при небольших (порядка нескольких метров) расстояниях между точками их провеса. В больших пролетах жесткостью проводов и тросов пренебрегают и рассматривают их как идеальные гибкие нити.
Расстояние по горизонтали между точками подвеса А и В называют пролетом и обозначают буквой l. Расстояние по вертикали в середине пролета между проводом и прямой АВ, соединяющей точки подвеса, называют стрелой провеса и обозначают буквой l. Обе величины измеряют в метрах.
Усилие, действующее вдоль провода, называют натяжением и обозначают буквой Т. Натяжение в проводах, рассматриваемых как идеальные гибкие нити, которые не могут воспринимать изгибающие моменты, обусловлено только растяжением и направлено по касательной и кривой провисания нити в рассматриваемой точке пролета. Натяжение в низшей точке кривой провисания проводов будет направлено горизонтально, его обычно обозначают буквой H.
При расчетах гибких нитей с малыми стрелами провеса считают также, что вертикальная нагрузка распределена равномерно не по длине самой нити (рис. 6.1, а), а по горизонтальной проекции нити (рис. 6.1, б); нить с такой нагрузкой провисает по параболе. Такое допущение вызывает малые погрешности и в то же время дает возможность значительно упростить расчет.
Натяжение провода Т изменяется в пролете от наименьшего значения Т — Н в низшей точке провеса провода до наибольшего значения у опор, равного
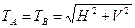
Так как V = 0,5 ql (см. рис. 6.1, б), то
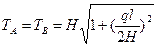
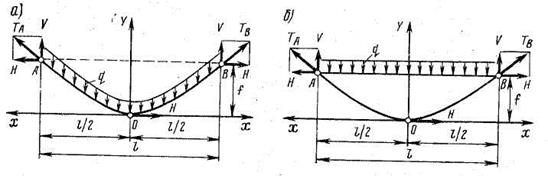
Рис. 6.1 Кривые провисания провода в пролете:
а — цепная линия; 6 — парабола
Провода и тросы контактных сетей электрифицированных железных дорог представляют собой гибкие нити, имеющие малые стрелы провеса по отношению к длине пролета. В таких нитях значение максимального натяжения Т мало отличается от натяжения нити Н. Если, например, f/l = 1/40, то разница в натяжении будет составлять всего 0,5 %. Поэтому при расчете нитей с малыми стрелами провеса (их еще иногда называют пологими нитями) часто считают, что натяжение нити постоянно и равно H.
Силу, действующую на единицу площади сечения провода, называют напряжением и обозначают буквой σ. Согласно определению σ = H/S (здесь S — площадь сечения провода).
Представим себе гибкую нить с опорами, расположенными на одном уровне, нагруженную произвольной вертикальной нагрузкой, распределенной по длине горизонтальной проекции нити (рис. 6.2, а). Показанные на этом рисунке реакции определим на основании уравнений статики. Так, сумма проекций всех сил на горизонтальную ось Σx= HA + HB = 0, откуда следует HA = HB = H.
Суммы моментов всех сил относительно опор В и А:
ΣMB=VA l- ΣMqB=0; ΣMA=VB l- ΣMqA=0.
В этих уравнениях ΣMqB и ΣMqA —моменты действующих на нить всех внешних заданных сил qx относительно опор В и А.
Из выше приведенных уравнений получим соответственно:
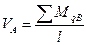 ;
; 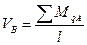 .
.
В случае определения реакций балки, показанной на рис. 6.2, б нагруженной точно так же, как нить, и имеющей такой же пролет, были бы получены такие же реакции, как по предыдущим формулам.
Таким образом, вертикальные составляющие опорных реакций нити равны опорным реакциям в простой балке АВ (см. рис. 6.2, б), нагруженной точно так же, как заданная нить. Подобные реакции будем в дальнейшем называть балочными.
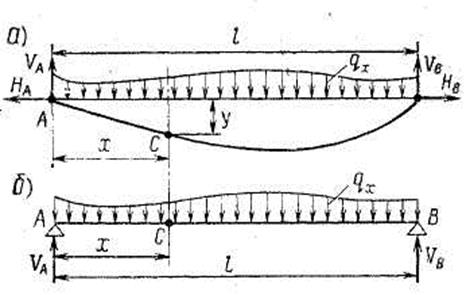
Рис. 6.2 Расчетные схемы гибкой нити, нагруженной произвольной вертикальной нагрузкой
Рассмотрим некоторое сечение нити в точке С на расстоянии х от левой опоры. Ордината этого сечения равна у (см рис. 6.2, а). Поскольку нить предполагается абсолютно гибкой, момент всех сил, действующих на нее по одну сторону от сечения, должен равняться нулю, т. е.
Mx – Hy = 0
где М х — сумма моментов всех вертикальных сил (включая и опорную реакцию),
расположенных левее сечения С;
Н — натяжение нити;
у — провес нити в точке С.
Момент Мх представляет собой не что иное, как изгибающий момент 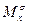 в соответствующем сечении простой балки. Подобные моменты будем в дальнейшем называть балочными. Уравнение может быть переписано в виде Мx = Ну, откуда имеем
в соответствующем сечении простой балки. Подобные моменты будем в дальнейшем называть балочными. Уравнение может быть переписано в виде Мx = Ну, откуда имеем
y = Mx/H
Данная формула представляет уравнение провисания гибкой нити. С помощью этого уравнения можно найти провес нити в любом ее сечении. По формуле можно также определить натяжение нити, если известен ее провес в каком-то сечении:
H = Mx /y
Рассмотрим одну из наиболее распространенных задач в теории гибких нитей — задачу об определении стрелы провеса и натяжения симметричной нити от нагрузки q, равномерно распределенной по всему пролету (рис. 6.3, а). Для этого случая балочные реакции VА и VВ равны (рис. 6.3, б), т. е. VА = VB = 0,5 q.
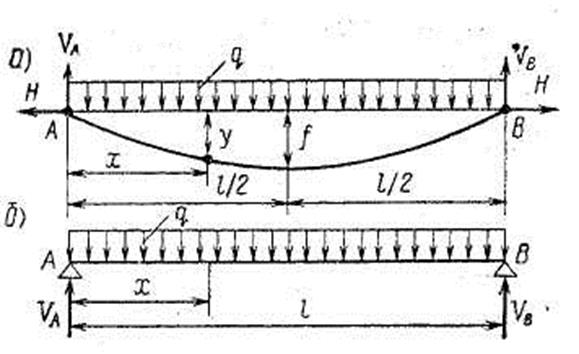
Рис. 6.3 Расчетные схемы гибкой нити, нагруженной равномерно распределенной по пролету нагрузкой
Балочный изгибающий момент Мх в сечении нити на расстоянии х от опоры А
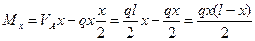
Подставив это значение Мх в выражение, получим уравнение провисания (равновесия) свободно подвешенного провода
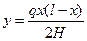
Для х = 0,5 l величина у = f, и формула примет вид
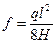
или
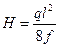
Подставив это значение H в формулу, получим
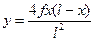
Длина провода в пролете может быть определена по формуле длины параболы. Длина отрезка одной ветви параболы от вершины О до точки с координатами (х, y)
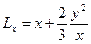
Для одной ветви параболы, изображенной на рис. 6.1, б, при х = 0,5 l и у = f получим
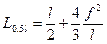
длина обеих ветвей параболы, т. е. длина провода в пролете
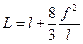
В некоторых случаях удобнее пользоваться формулой для определения длины провода, в которую входит не стрела f, а величины q и H.
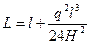
Преобразуя, получим выражение для расчета натяжения свободно подвешенного провода у опор:
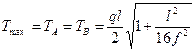
 2015-06-05
2015-06-05 14602
14602







