Если алгебраическое или трансцендентное уравнение достаточно сложно, то его сравнительно редко удается решить аналитическими методами. Более того, в некоторых случаях коэффициенты уравнения известны лишь приближенно, и сама задача о точном определении корней теряет смысл. Поэтому важное значение приобретают способы приближенного нахождения корней уравнения и оценки их точности. Пусть дано уравнение:
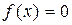 ,
,
где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале 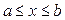 . Всякое значение ξ, обращающее функцию f(x) в нуль, т.е. такое, что f(ξ) = 0, называется корнем уравнения. Будем предполагать, что уравнение имеет лишь изолированные корни, т.е. для каждого из них существует окрестность D, не содержащая другие корни (рис. 26). Решить уравнение численными методами – это значит определить, имеет ли оно корни, сколько их и найти корни с заранее заданной точностью. Для решения уравнений вида разработано много различных итерационных методов. Сущность этих методов заключается в следующем.
. Всякое значение ξ, обращающее функцию f(x) в нуль, т.е. такое, что f(ξ) = 0, называется корнем уравнения. Будем предполагать, что уравнение имеет лишь изолированные корни, т.е. для каждого из них существует окрестность D, не содержащая другие корни (рис. 26). Решить уравнение численными методами – это значит определить, имеет ли оно корни, сколько их и найти корни с заранее заданной точностью. Для решения уравнений вида разработано много различных итерационных методов. Сущность этих методов заключается в следующем.

Рисунок 26 – Решение уравнения
Пусть известна достаточно малая область D, в которой содержится единственный корень ξ уравнения. В этой области выбирается точка x0 – начальное приближение – и строится последовательность точек x1,x2,…xn,…, сходящаяся к ξ, с помощью некоторого рекуррентного соотношения:
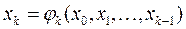 .
.
Рекуррентное вычисление повторяется до тех пор, пока абсолютное значение разницы между двумя последовательными значениями х не станет меньше некоторого значения е, называемого точностью:
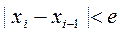 .
.
Выбирая различными способами функции φk, которые зависят от функции f и номера k, можно получить различные методы.
Численное решение нелинейных уравнений
методом итерации
Заменим уравнение
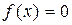
равносильным ему уравнением
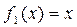 .
.
И исходное и полученное уравнения имеют одинаковый корень x (рис. 27) и называются эквивалентными.
Выберем любым способом х0, которое затем подставим в левую часть уравнения:
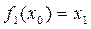 .
.
Полученное значение х1 снова подставим в левую часть и получим:
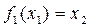 .
.
Продолжая этот процесс, получим последовательность чисел х1, х2,..., xn, которая может либо сходиться, т.е. иметь предел, либо расходиться, т.е. не иметь предела. Тогда в соответствии с полученным результатом в первом случае этот предел является корнем уравнения (х ® x), во втором случае сделаем вывод о невозможности получения решения данным способом.
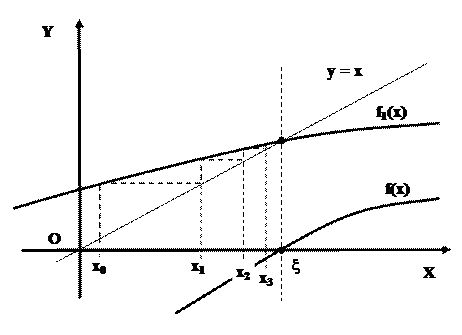
Рисунок 27 – Геометрическая интерпретация итерационного метода решения уравнения
Алгоритм реализации данного метода будет схож с алгоритмом рекуррентного вычисления бесконечной суммы.
Приведём программу, реализующую итерационный метод уточнения корня уравнения:
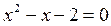 .
.
program Iter;
VAR
xp, e, x0, x:REAL;
Function f(x:real): real;
Begin
f:= x*x-2;
end;
Begin
writeln('введите начальное приближение х и точность');
read(x0,e);
x:=x0;
REPEAT
xp:=x;
x:=f(x);
UNTIL ABS(x-xp)<e;
writeln('корень уравнения =', x);
End.
В данной программе используется подпрограмма функция f, которая вычисляет левую часть преобразованного уравнения:
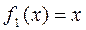 .
.
Переменная xp используется в программе для сохранения предыдущего значения х.
Численное решение нелинейных уравнений
методом бисекции
Метод состоит в построении последовательности вложенных отрезков, на концах которых F(х) имеет разные знаки. Каждый последующий отрезок получают делением пополам предыдущего. Этот процесс построения последовательности вложенных отрезков позволяет найти нуль функции (F(х) = 0) с любой заданной точностью.
Опишем подробно один шаг итерации (рис. 28). Пусть на k-м шаге найден отрезок [аk, bk], на концах которого F(х) меняет знак. Заметим, что обязательно [аk, bk] Î [а, b].
1. Разделим теперь отрезок [аk, bk] пополам и выделим F(ck), где ck – середина [аk, bk].
2. Здесь возможны два случая:
§ первый, когда F(ck) = 0, тогда мы говорим, что корень найден;
§ второй, когда F(ck) ¹ 0, тогда сравниваем знак F(ck) с F(аk) и F(bk) и из двух половин [аk, ck] и [ck, bk] выбираем ту, на концах которой функция меняет свой знак. Таким образом, аk+1 = аk, bk+1 = ck, если F(ck)F(аk) < 0 (рис. 27), и аk+1 = ck, bk+1 = bk, если F(ck)F(bk) < 0.
При заданной точности e деление пополам продолжают до тех пор, пока длина отрезка не станет меньше 2e, тогда координата середины последнего найденного отрезка и есть значение корня требуемой точности.
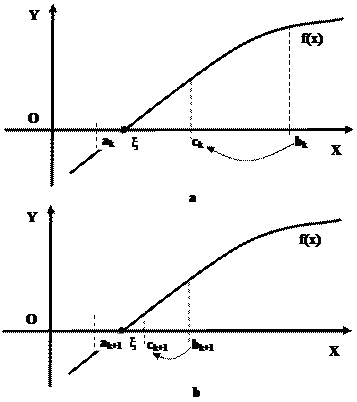
Рисунок 28 – Геометрическая интерпретация решения уравнения методом бисекции
a) k–й шаг; b) k+1-й шаг.
Приведём программу, реализующую итерационный метод уточнения корня уравнения:
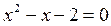 .
.
program Bisect;
VAR
A,B,E:REAL; X: REAL;
Function f(x:real): real;
Begin
f:= x*x-x-2;
end;
Begin
writeln('введите отрезок локализации корня [a,b] и точность');
read(a,b,e);
k:=0;
REPEAT
X:= (A+B)*0.5;
IF f(X)*f(B)<0 THEN
a:=x
Else
b:=x
UNTIL ABS(B-A)<e;
writeln('корень уравнения =', (A+B)*0.5);
END.
В данной программе используется подпрограмма функция f, которая вычисляет левую часть исходного уравнения:
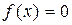 .
.
Переменная x используется в программе для сохранения значения середины отрезка [a, b].
Численное решение нелинейных уравнений
методом Ньютона
Положим:
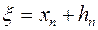 ,
,
где x – корень уравнения f(x) = 0, hn считаем малой величиной. Отсюда, применяя формулу Тейлора, получим:
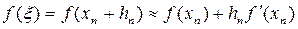 .
.
Следовательно, 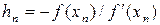 . Подставив это выражение, получим:
. Подставив это выражение, получим:
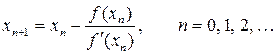
Геометрическая интерпретация метода представлена на рисунке 29.
Через точку А0(х,у) с координатами х = x0, у = f(x0) проводим касательную. По формуле
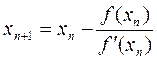
находим точку пересечения касательной с осью ОХ (точка х1).
Находим точку А1(х1,у), проводим касательную через точку А1 для нахождения х2.
Этот процесс продолжаем до тех пор, пока разница |хi+1-xi| не станет меньше, чем значение e, т.е. пока не будет найдено значение корня с заданной точностью e.

Рисунок 29 – Геометрическая интерпретация решения уравнения методом Ньютона
Приведём программу, реализующую итерационный метод уточнения корня уравнения:
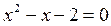 .
.
program Newton;
VAR xp,E,x0:REAL; X: REAL;
Function f(x:real): real;
Begin
f:= x*x-x-2;
end;
Function df(x:real): real;
Begin
df:= 2*x-1;
end;
Begin
writeln('введите начальное приближение х и точность');
read(x0,e);
x:=x0;
REPEAT
xp:=x;
x:=x-f(x)/df(x);
UNTIL ABS(x-xp)<E;
writeln('корень уравнения =', x);
END.
В данной программе используется подпрограмма функция f, которая вычисляет левую часть исходного уравнения:
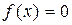
а также подпрограмма функция df, которая вычисляет значение дифференциала:
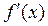 .
.
Переменная xp используется в программе для сохранения предыдущего значения х.
 2015-06-05
2015-06-05 645
645








