Численное интегрирование методом Симпсона с заданной точностью

Принцип метода Симпсона состоит в замене под­ын­те­граль­ной функ­ции f(х) интерполяционным мно­гочленом Нью­­то­на вто­рой сте­пени. Тогда для каждого эле­мен­тар­­но­го от­резка [хi,хi+1] име­ем следующее значение площади подынтегральной кривой:

^.

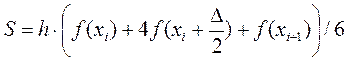Для всего отрезка интегрирования [a,b] формулой Симпсона:

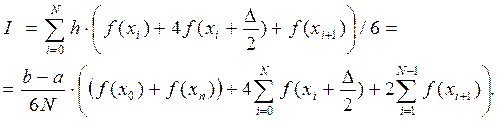
Данное выражение называется формулой Сим­сона. Оно от­носится к формулам по­вы­шен­ной точ­нос­ти и яв­ля­ется точ­ной для мно­го­чле­нов второй и третьей сте­пе­ни.

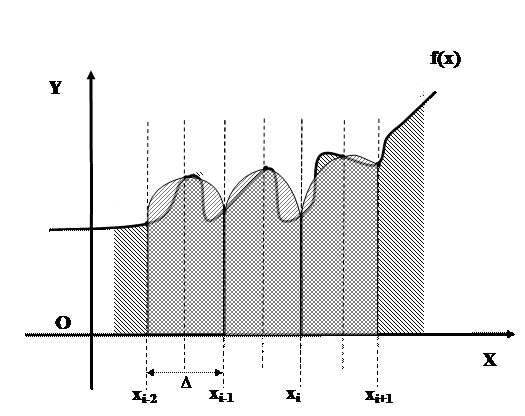
Рисунок 31 – Геометрическая интерпретация численного интегрирования методом Симпсона

Приведём программу, реализующую вычисление определённого интеграла методом Симпсона с заданнойточностью. В качестве подынтегральной будем использовать функцию:

^.

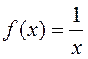Рассмотренные формулы численного интегрирования требуют чёткого указания количества разбиений отрезка интегрирования. Однако классическое использование численного метода предполагает вычисление значения (корня, интеграла и т.д.) с заданной точностью.

Точность любой формулы численного интегрирования зависит от величины отрезка разбиения D.

Будем вычислять значение интеграла при разных значениях D (D₁, D_2, D_3,…), где D_i+1 = 2D_i. Как только разница между значением интеграла, вычисленного при D_i и интеграла, вычисленного при D_i+1, станет меньше, чем значение e, будем считать, что интеграл вычислен с заданной точностью e.

Данный метод интегрирования с заданной точностью прост в реализации, однако он требует значительных избыточных вычислений, что приводит к повышению затрат времени на вычисление.

program simp;

function f(x: real): real;

Begin

f:=1/x

end;

Var

a,b,e: real;

i: integer;

xa,xab,xb,dx,s1,s: real;

n: integer;

Begin

writeln('[a,b],e');

readln(a,b,e);

{вычисление интеграла с количеством разбиений равным 1, т. е. одной фигурой с основанием равным [a,b]}

n:=1;

dx:=(b-a)/n;

s:=dx*(f(a)+4*f(a+dx/2)+f(b))/6;

Repeat

n:=n*2; {удвоение количества отрезков разбиения}

s1:=s;

s:=0;

{вычисление длины отрезка – основания прямоугольника (дельта) при новом количестве разбиений}

dx:=(b-a)/n;

{суммирование площадей - нахождение интеграла при заданном количестве разбиений}

for i:=0 to n-1 do

Begin

xa:=a+dx*(i);

xb:=xa+dx;

xab:=xa+dx/2;

s:=s+dx*(f(xa)+4*f(xab)+f(xb))/6;

end;

until abs(s-s1)<=abs(e);

writeln('int=',s);

End.

В данной программе используется подпрограмма функция f, которая вычисляет подынтегральную функцию .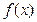

Переменная s1 используется для сохранения значения интеграла, вычисленного при вдвое меньшем количестве разбиений.