Протокол от 22/Ш 1956 г. Исп. А. П

Обратить Юм в миллиметры¹. 10 м-10 = 100 дм 100 дм = 10000 мм. Обратить 15 м в миллиметры. 15 м = 15 000 мм. Обратить 25 дм в миллиметры. 25 дм = 25 ■ 10=250см ■ 10=2 500мм. Обратить 350дм в миллиметры. 350 дм = 350 дм 100 = 35 000 мм. Обратить 5,2 дм в миллиметры. 5,2 дм = 100 мм -5,2 = 520 мм. Обратить 2,7 дм в миллиметры. 2,7 дм = 270 мм. Обратить 320мм в дециметры. 320мм = 3,2 дм.

Как видно из протокола, первоначальные задания «обратить метры в миллиметры» и «обратить дециметры в миллиметры» выполняются с помощью опосредующей системы значений и действий умножения.

Ученик сначала обращает метры в дециметры, а затем дециметры в миллиметры. Такой путь выделения нового значения является закономерным. Подобно этому происходит процесс обращения дециметров в миллиметры: ученик сначала обращает дециметры в сантиметры, а затем сантиметры в миллиметры. Для превращения одного значения в другое ученик использует третье значение, которое связано с данным и искомым значениями и выступает как средство анализа данного значения на основе искомого. Анализ, который проделывается учеником, осуществляется здесь в системе действий умножения или деления, позволяющих (с помощью третьего значения) преобразовать данное в искомое, найти неизвестное, новое значение че- рез известное. Как отсут ствие известного (третьего) значе-

¹ В заданиях вместо понятий «раздробление» и «превращение», связанных для учащихся с определенными действиями, использовалось понятие «обращение».

ния, так и отсутствие необходимых действий не позволило бы произвести анализ.

В результате анализа отношений между данными и искомым заданная мера длины приобретает новое значение. Так, в решении первой задачи метр приобретает значение 1000 мм. Естественно, что при решении новой задачи ученик прямо использует это новое значение¹.

Однако такое использование вновь выделенного значения происходит не всегда. В приведенном протоколе можно видеть, что после анализа двухзначного числа, выражающего дециметры, ученик вновь анализирует те же отношения, если величина значения выражена трехзначным или дробным числом.

В процессе анализа наряду с существенными отношениями, характеризующими новое значение метра, выделяются также и несущественные отношения, составляющие конкретную величину данного значения (например, 15 метров, 0,2 дециметра и т. п.). Поэтому изменение конкретной величины значения требует нового процесса анализа.

Подобно этому анализ одного значения, например дециметра в его отношении к миллиметру, не означает еще, что здесь устанавливается также и новое значение миллиметра.

Процесс выделения существенных отношений, составляющих новое значение (соответствующих определенному уровню обобщения), включает отвлечение от конкретной величины определенных мер длины, т. е. выделение этих отношении между единицами измерения. Во второй серии экспер иментов это было сделано путем

¹ На основании того, что в рассматриваемом случае необходимым элементом выделения нового значения является преобразование одного значения в другое (с помощью действий умножения или деления), может показаться, что суть происходящего процесса и заключается в этом преобразовании. Однако при таком объяснении нельзя понять ни необходимости в новых «преобразованиях» при изменении условий задания, ни возможности «непосредственного» обращения одних мер измерения в другие, т. е. условий «выпадения» как опосредующих значений, так и действий преобразования.

Суть проблемы заключается здесь в закономерностях процесса познания, приводящего к изменению действия, а не в самих по себе модификациях действия.

Другое дело, что вне действия (равно как и без опосредующих значений) невозможно раскрыть новые отношения. Но эти действия не представляют в процессе мышления чего-либо специфического, они равно могут использоваться в других случаях и выпадают по мере установления общих существенных отношений, т. е. по мере продвижения мышления на более высокую ступень.

специального выделения в заданиях единиц измерения (1 метр, 1 дециметр и т. д.) и отношений между ними.

При решении таких задач происходит выделение нового значения как бы в его «чистом виде», что позволяет испытуемому в дальнейшем использовать новое значение в решении любой конкретной задачи.

Как показали эксперименты, решение такой специальной задачи, в которой нужно определить количество миллиметров в одном метре или одном дециметре, также требует опосредующей системы значений. Но в отличие от ранее описанного процесса применения вновь выделенного значения в условиях конкретной задачи теперь новое значение единицы измерения используется без предварительного анализа данных величин. При выделении нового значения единиц измерения раскрываются существенные отношения, общие для всех конкретных величин; т. е. в этом случае выделяется не только новое значение данной меры длины, но ее новое обобщенное значение, абстрагированное от конкретной величины единиц измерения. Это позволяет испытуемому применять выделенное значение в условиях новых задач без предварительного анализа конкретных данных этих задач (происходит «перенос»).

Анализ результатов второй части исследования показал следующее:

1. Процесс выделения новых значений опосредован системой известных человеку значений, связанных с данными и искомыми значениями. Известные испытуемому значения, выражая отношения между данным и искомым значением (например, в десять раз больше (меньше), определяют действия (умножения и деления) по преобразованию данного значения в требуемое.

2. Результатом выделения нового значения является возможность выполнения сходных заданий (обращения одной меры длины в другую) без опосредующей системы значений и связанных с ними действий. Действия, с помощью которых осуществлялся анализ новых отношений и которые служили формированию нового значения, естественно, выпадают. Они применяются в новых или сложных условиях, требующих анализа.

3. В решении конкретных задач на обращение одной меры длины в другую происходит выделение как существенных отношений (между единицами мер дли-

ны), так и несущественных (между конкретными величинами мер длины). Лишь в результате выполнения ряда заданий с различными конкретными величинами происходит их абстрагирование, достигается обобщение, на основе которого испытуемый может выполнять любые новые сходные задания, не используя средств анализа. Выполнение заданий на обращение, в которых в качестве первоначальных значений даны единицы мер длины, позволяет сразу выделить существенные отношения и достигнуть обобщения.

Мы рассмотрели последовательно две основные стороны, характеризующие процесс анализа:

а) функциональную роль различных элементов условий задания, предложенного субъекту;

б) возможности субъекта, выражающиеся в применяемых им средствах анализа.

Надо полагать, что результаты проведенных экспериментов имеют отношение к педагогической практике, к методике обучения.

Методисты и педагоги неоднократно рекомендовали строить процесс обучения путем постановки перед учениками «задач». Эффективность постановки предварительных задач в процессе объяснения учебного материала показана и в ряде психологических исследований.

Приведем один пример из наших опытов на материале геометрии.

Теорему о сумме внутренних углов треугольника можно объяснять учащимся различными способами. Один из способов заключается в том, чтобы последовательно доказать, что сумма углов равна 2d (180°). Однако, как известно из педагогической практики, такой способ обучения часто ведет к формальным знаниям. Возможен и другой способ. Он заключается в том, что перед учеником ставится такое задание, которое ведет к возникновению проблемной ситуации, вызывает необходимость в анализе условий задания.

Для объяснения этой теоремы мы ставили перед учащимися первоначально такое задание: построить треугольник по трем данным углам; их сумма составляла меньше или больше 180°. Например ZA=60°, ZB=43°

и ZC=20° или ZA=80°, ZB=50° и ZC=70°. Естественно, что в этих условиях учащиеся не могли построить треугольник, перед ними возникала проблемная ситуация, возникала необходимость в выяснении причин невозможности выполнения задания, возникала потребность в анализе закономерности, заключенной в этой теореме.

Можно выделить два основных пути создания условий для возникновения проблемной ситуации перед учащимися в школьной практике.

Первый путь заключается в создании таких условий в практической деятельности учащихся, которые требуют выделения тех или иных закономерностей, необходимых для правильного осуществления этой деятельности. Этот путь можно считать типичным для изучения таких учебных предметов, которые имеют прямую связь с теми или иными видами практической деятельности и в первую очередь трудовой (физика, математика, химия, биология и др.).

Второй путь создания условий для возникновения проблемной ситуации заключается в требовании объяснить те или иные изучаемые явления (например, исторические факты).

Одним из конкретных способов создания условий, вызывающих проблемную ситуацию, может быть способ использования явно ошибочных условий, в результате которых учащиеся не могут выполнить задания (как в приведенном выше примере).

Рассматривая роль и место средств анализа в процессе обучения, можно привести много примеров из школьной жизни, показывающих характер и необходимость «опосредования» в процессе усвоения знаний.

Например, с помощью линейных мер невозможно измерить площадь, однако в качестве начальных единиц измерения мы используем именно их, определяя длину и ширину в линейных единицах. Способ преобразования одних значений в другие здесь, как известно, заключен в умножении. Однако само умножение как способ было бы бессмысленным и иногда именно так и выступает, ибо оно приобретает свой смысл только через выделение «единиц площади» — квадратов, однозначно определяемых линейными единицами. Без этого «опосредования» невозможно полноценно усвоить способ определения площади.

Выделение средств анализа указывает путь использования наличных знаний и «опыта» ученика в процессе обуче-

ния его новым знаниям. Одновременно понятие «средств» анализа характеризует возможности и границы такого использования.

Мы специально разделили условия и средства анализа и рассмотрели их отдельно. В реальном процессе, как мы уже отмечали, сами средства анализа выступают как одно из условий осуществления анализа.

Литература

1. Анциферова Л. И. Роль анализа в познании причинно-следственных отношений // Процессы мышления и закономерности анализа, синтеза и обобщения: Сб. науч. тр. — М., 1960.

2. Выготский Л. С. Мышление и речь // Избранные психологические исследования. — М.: Изд-во АПН РСФСР, 1956.

3. Богоявленский Д. Н. Психология усвоения знаний в школе / Д. Н. Богоявленский, Н. А. Менчинская. — М.: Изд-во АПН РСФСР, 1959.

4. Ленард Ф. Количества в математике / Ф. Ленард, А. Чор // Математика в школе. — 1959. — № 3.

5. Леонтьев А. Н. Опыт экспериментального исследования мышления// Доклады на совещании по вопросам психологии. — 1954.

6. Матюшкин А. М. Об условиях возникновения анализа // Доклады АПН РСФСР. - 1959.

7. Пономарев Я. А. Взаимоотношение прямого (осознаваемого) и побочного (неосознаваемого) продуктов действия // Вопросы психологии. - 1959. - № 4.

8. Рубинштейн С. Л. О мышлении и путях его исследования. — М.: Изд-во АН СССР, 1958 - Т. 1.

9. Рубинштейн С. Л. Принцип детерминизма и психологическая теория мышления // Психологическая наука в СССР: Сб. науч. тр. — М.: Изд-во АПН РСФСР, 1958.

10. Шеварев П. А. Обобщенные ассоциации в учебной работе школьника. - М.: Изд-во АПН РСФСР, 1959.

11. Duncker К. A qualitative (experimental and theoritical) study of productive thinking (solving of comprehensive problems) // J. genetic, psychology. — 1926.-Vol. 33.-№4.

12. Duncker K. On problem-solving// Psychol, monographs. — N. -Y., 1945. — Vol. 58. - №5 (Whole № 270).

13. MaierN. R. F. Reasoning in humans. 1. On direction. J. сотр. psychology, 1930.

14. Ruger H. A. The psychology of efficiency // Arch, psychology. — 1910. — Vol.2.-№15.

15. Szekely L. Studien zur Psychologie des Denkens: zur Topologic des einfalls//Acta psychologica. — 1940. — № 5.

16. Szekely L. The dynamic of thought motivation // American J. psychology. — 1943. -Vol. 56. -№1.

17. Szekely L. Productive processes in learning and thinking // Acta psychologica. — 1950. — № 7.

18. Szekely 1. Knowledge and thinking // Acta psychologica. — 1950. — № 7.

19. WertheimerM. Productive thinking. — N.-Y: Harper, 1945.

Анализ и обобщение отношений.

К характеристике анализа в процессе

обобщения отношений

Задачей нашей работы являлось исследование зависимости обобщения отношений от процесса анализа.

В качестве материала для экспериментального исследования были взяты позиционные системы счисления.

Системой счисления называется совокупность немногих названий и знаков, позволяющих обозначать любое число. В позиционных системах счисления при обозначении числа имеет значение не только сама цифра, но и занимаемое ею место в числе (позиция). Позиция цифры в числе указывает на содержание единицы разряда, а цифра является как бы его коэффициентом. При отсутствии того или иного разряда ставится «О». В основе построения числа в позиционной системе счисления лежит закономерность, включающая ряд отношений. Если эти отношения выразить формулой, то любое число любой позиционной системы счисления можно представить как

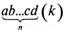^а-к"-¹ +b-k"-²+... + c-k+d,

где а, Ь, с, d —любые цифры числа, «А» — основание системы счисления, а п — количество цифр и числе. Закономерность построения числа в позиционной системе счисления, таким образом, включает в себя отношение между основанием системы счисления и местом цифры в числе, выражаемое в формуле зависимостью между кип (мультипликативный принцип образования разрядов числа) и отношение, составляющее способ образования разрядов в числе с помощью сложения (аддитивный принцип). Основой закономерности построения числа в позиционной системе счисления является принцип образования единиц разрядов. Основание системы счисления, умноженное на единицу разряда, составляет одну единицу следующего, высшего разряда.

Каждый человек, обучавшийся в школе, знаком с десятичной позиционной системой счисления, которая в настоящее время принята в большинстве стран. Основанием десятичной системы счисления, выраженным в единице второго разряда, является число 10. Любое число десятичной системы счисления можно выразить как

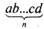(10)=а-10^л"¹ +ЬЛ0"-² +... + c-lQ + d,

(например, 4 325 = 4-10⁴¹+ 3-Ю⁴"² + 2-Ю⁴³ + 5).

Для обозначения любого числа в десятичной системе требуется десять знаков — цифр (1, 2, 3, 4, 5, 6, 7, 8, 9, 0).

Другие позиционные системы счисления отличаются от десятичной по своему основанию (единице второго разряда) и количеству цифр, необходимых для обозначения числа. Если взять пятеричную систему счисления, то любое число в ней можно выразить как

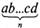(5)=a-5"-^l+b-5ⁿ-²+...+c-5+d,

(например, 3 214 = 3-5³ +2-5² + 1-5 + 4). Для обозначения любого числа в пятеричной системе счисления достаточно пяти цифр.

Таким образом, в основе построения числа в любой позиционной системе счисления лежит одна и та же закономерность, составляющая позиционный принцип. Это позволило нам использовать позиционные системы счисления как экспериментальный материал для исследования процесса формирования обобщения.

В средней школе дети не изучают недесятичные позиционные системы счисления, поэтому можно было использовать в экспериментах другие системы счисления как новый материал. Это позволило избежать обычной трудности экспериментального исследования процесса мышления — искусственных построений, систем, создаваемых специально для эксперимента.

Эксперименты носили характер последовательного решения испытуемым системы задач, требующих выделения отношений, составляющих закономерность, и соответствующих действий обозначения числа, основанных на этих отношениях.

Было проведено три серии экспериментов.

В первой серии экспериментов от испытуемого требовалось сначала найти формулу числа в десятичной системе. Затем испытуемый должен был обозначать числа в условиях пятеричной системы счисления. Второе задание являлось контрольным и позволяло проверить характер обобщения, достигнутого испытуемым. В тех же случаях, когда испытуемый не мог выполнить сразу второго задания, оно служило процессу обобщения, а контрольным заданием тогда являлось обозначение числа в других недесятичных системах счисления.

Во второй серии экспериментов от испытуемого первоначально требовалось обозначать числа в новой (пятеричной) системе счисления, а так как испытуемый не мог выполнить этого задания, то ему предлагалось найти формулу числа в десятичной системе, чтобы на этой основе обозначать числа в пятеричной системе.

Контрольным заданием здесь также являлось обозначение числа в условиях других позиционных систем счисления.

В третьей серии экспериментов от испытуемого требовалось не только найти формулу числа в десятичной системе (как в первой серии), но и обосновать выделенные в формуле отношения. Контрольное задание оставалось прежним.

Таким образом, в излагаемых сериях экспериментов изменялись условия и пути процесса анализа, приводящего к обобщению, что естественно изменяло и характер самого процесса обобщения.

Для обозначения чисел недесятичных систем счисления в экспериментах использовались цифры и названия, взятые из десятичной системы счисления. Испытуемыми являлись студенты и аспиранты, не изучавшие специальных курсов по теории числа и не знакомые с другими системами счисления, кроме десятичной.

В экспериментах приняло участие 45 человек (по 15 человек в каждой серии).

В предварительных экспериментах перед испытуемым ставилось задание, требующее обозначить число в пятеричной системе счисления с помощью пяти цифр (1, 2, 3, 4, 0). Все испытуемые владели способом обозначения числа в десятичной системе. Несмотря на это, ни

один из них не мог выполнить поставленного задания, т. е. использовать известный ему общий способ построения числа в позиционной системе счисления в новых условиях при изменении основания позиционной системы. Выполнение задания потребовало от испытуемых длительного и сложного процесса анализа новых условий обозначения, в котором раскрывалась закономерность построения числа в условиях пятеричной системы счисления.

Было выдвинуто предположение, что испытуемый не может использовать известного ему способа обозначения в новых условиях по той причине, что в процессе анализа он не достиг необходимого уровня обобщения отношений, лежащих в основе требуемого нового способа обозначения. Для проверки этого предположения была проведена первая серия экспериментов.

Обобщение отношений на основе

предварительного выделения формулы

числа в десятичной системе

В первой серии экспериментов перед испытуемым вначале ставилась задача найти формулу любого числа в десятичной системе.

В процессе решения этой задачи (включающей ряд частных задач) испытуемый раскрывал отношения, составляющие закономерность построения числа в десятичной системе и включающие принцип построения числа в любой позиционной системе счисления.

Перед испытуемым ставилось задание обозначать числа в пятеричной системе счисления, т. е. с помощью пяти цифр (1,2, 3,4,0).

Новое задание требовало от испытуемого использования той закономерности, которая была им выделена в процессе анализа десятичной системы и выражена в формуле любого числа десятичной системы.

Можно было ожидать, что испытуемый использует выделенную закономерность построения числа в новых условиях.

Рассмотрим типичный протокол экспериментов.

Протокол № 30 от 3.01.1957 г.

Эксп. В школе Вы учили десятичную систему счисления. Сейчас давайте проверим, как хорошо Вы ее знаете. Напишите число 1 233 489. Исп. (Пишет). Эксп. Очень хорошо. Напишите формулу числа 1ТЛ1, т. е. числа, вы-

п

раженного с помощью единиц, где «л» обозначает любое количество единиц в числе.

Исп. Никак не могу понять, как можно написать такую формулу. Ведь это не сумма «л» единиц?.. Или, если взять единицу «л» раз, тогда опять только сумма единиц... Нет, ничего не получается. Если я так буду решать задачи, то у меня ничего не выйдет. Может быть мне лучше уже не начинать?

Эксп. Давайте сначала найдем формулу для числа KXLI), где «/я» обозначает любое количество нулей. т

Исп. Так это не легче. Вся трудность в том, что нулей может быть любое число.

Эксп. Решите эту задачу для случая, где т = 5.

Исп. Значит, пять нулей — 100.000.

Ага, посмотрим — 10,100... Так... Когда я прибавляю один нуль, тогда число увеличивается в 10 раз. Здесь будет 10⁵, а 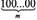" "" = 10™.

Нос единицами так не пойдет. Возьмем 11,111,1111... Какая же здесь соблюдается последовательность? Никакой последовательности не вижу. Как же здесь разобрать?

Эксп. Допустим, что л = 5. Напишите, чему равна каждая единица в этом числе.

Исп. 11 111 = 10 000 + 1 000 + 100 + 10 + 1... Ну, теперь просто. 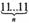= Г = Г~'... Нет, опять не получается. Понятно, ведь здесь нужно

брать 10, а не единицу... 10" + 10"^-1 + Ю""² + 10+1. Но это ведь для данного числа, а п как же для любого? Здесь есть одна ошибка: л = 5, а нулей-то только четыре... 10"'+ 10""²... Для любого числа нужно обозначить точками, потому что показатель степени будет постоянно уменьшаться. 10"' + +10"-²... + 10+1.

Эксп. Теперь напишите формулу для любого числа десятичной систе- Mbiab...cd, где а, Ь, с, d— любые цифры, а «л» указывает на любое количество цифр.

Исп. Пусть л = 4, тогда будет оООО + 600 + сО + d, значит, 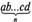= a-W-^l + b-lOⁿ'² +...+ c-lO+d.

Эксп. Проверьте эту формулу.

Исп. л = 5; а = 7; Ь = 4; с = 8; d = 3; 1 = 2.

70 000 + 4 000 + 800 + 30 + 2 = 7-10⁴ + 4-10³ + 8-10²+3-10 + 2 = 74 832.

Эксп. Теперь будем решать новую задачу. Кроме десятичной системы счисления существуют еще и другие, недесятичные. Сейчас нам нужно будет писать числа в пятеричной системе счисления. Для обозначения любого числа здесь достаточно пяти цифр — 1, 2, 3, 4,0... Напишите число 17.

Исп. А можно ли складывать или умножать?

Эксп. Нет, знаками действия пользоваться нельзя.

Исп. Здесь должна быть какая-то система, какой-то принцип. Цели я напишу так же, как в десятичной системе, например, один и два (12), то это будет двенадцать?

Эксп. Нет, это не будет двенадцать.

Исп. А зачем здесь дан нуль? Ведь 4 и 0 — это все равно не будет сорок. «0» в десятичной системе показывает место цифры, а здесь он зачем? Складывать нельзя, вычитать нельзя, что же делать? Ведь это отдельные цифры, которые не имеют никакой системы.

Эксп. Сразу написать 17 трудно... Напишите 5.

Исп. Если я найду пятерку, я уже буду знать систему, тогда уже и делать нечего. Но сочетание двух цифр, вероятно, что-то обозначает? Может быть, цифры повторяются? Здесь, когда дальше нет цифр, должен начинаться второй ряд: 1, 2,3,4,0; 1,2,3,4,0. Это второй ряд. Посмотрим, как обозначается вторая единица в десятичной системе. Там единица и нуль — это десять. Выходит, что здесь единица с нулем — это будет пять. А как же дальше? Нет, к десятичной системе здесь не сведешь. Если на первом месте единица, а на втором два, то... Нет, если 2 просто, то 2 с нулем должно быть 6... Я никогда не слышал про пятеричную систему. Да собственно и десятичную систему я никогда не изучал, я не думал над ней... Когда я пишу 1 — это 1. Когда один с нулем — это 10. Здесь, когда 1 — это 1, когда 1 с нулем — это 5. В десятичной дальше две единицы — это одиннадцать. А здесь тогда 11 — это 6. Так, 12 = 7,13 = 8,14 = 9... Больше у меня цифр нет, значит дальше идет нуль... 100 = 10. Нет, если 14 = 9... напишем как в десятичной системе 10,11,12,13,14,15,16,17,18,19. Дальше цифр нет, мы пишем 20... 10 это 20. Вот и все. Я строю по десятичной системе 21 = 11; 22 = 12; 23 = 13; 24= 14; 25 = 15... Нет, 5 нет, значит 30 = 15; 31 = 16; 32=17.

Эксп. Напишите 38.

Исп. Здесь нужно найти систему, а то Вы, пожалуй, дадите написать какое-либо большое число... 5 = 10; 10 = 20: в два раза больше. А 24 = 14; 32 = 17... Нет, системы я еще не знаю... Возьмем 17 — это 3 пятерки и 2 = 32. 28 — это 7 пятерок и 3 = 73.

Эксп. А разве есть цифра 7?

Исп. Ах, да... Как же здесь? но 7 — это 12, тогда 38 — это 123.

Эксп. Напишите 149.

Исп. Все-таки 38 я нашел неудачно. Где же тут собака зарыта? 100 это 20 пятерок; 40 — это 8 пятерок; 9 — одна пятерка и 4. А что дальше? Нужно написать подряд хотя бы первую сотню. А если взять в пятеричной, например, 21 314, то сколько будет здесь? Это тоже задача. Здесь собственно нужно переводить из одной системы в другую. Опять нужна формула. Без нее ничего не сделаешь... Посмотрим, как же тут получается... (Далее испытуемый строит числовой ряд в пятеричной системе, записывая под каждым числом его значение в десятичной системе).

1 2 3 4 10 11 12 13 14 20 21 22 23 24 30 31 32 33 34 35 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Нет, «35 — это 20» неверно: ведь 5 нету... (продолжает строить числовой ряд).

40 41 42 43 44 45 20 21 22 23 24 25

Нет, опять нет 5... Здесь будет так:

100 101 102 103 104 ПО 111 112 113 114 120 121 122 123 124 130 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

Теперь посмотрим... 44 и единица — это пять пятерок, т. е. 25. Мы обозначаем это как 100... 100 — это 25 (в четыре раза больше)... Я устал немного. (Перерыв 3 минуты).

Возьмем основные числа: 5. 25... Дальше должно быть 125 и так далее... Это 5 в какой-то степени. И еще 5, 10, 15 и так до тысячи и дальше. Число 149 должно выглядеть так... Возьмем 1000 — это 125, а как же проверить?.. 1—5 (один нуль) — 25 (второй нуль)... Неужели придется писать до тысячи? Да, придется проверить... Еще один нуль (в тысяче — А. М.) — опять в пять раз больше. Ясно:

1000-это 125.

Найдем 1243 (см. выше. — А. М.).

Это будет 125 + 50 + 20 + 3 = 198. А нам нужно найти 149. Здесь надо идти обратным путем. 125 — это 1 000 и остается еще 24... 24 — это 44... 149 — это 1 044. Теперь я могу найти любое число, но формулы найти не могу.

Эксп. Найдите число 111(5).

Яси. 100 = 25; 11 =6; 1П₍5) = 31.

Эксп. Найдите число 1 111 ₍₅>

Исп. 1000= 125 и 31,1 111(5,= 156.

Эксп. Найдите число 111111(5).

Исп. 1 000 - 125; 10 000 = 125 х 5 = 625; 100 000 = 625 х 5 = 3 125;

111 111 = 3125 + 625+156=3 906.

Эксп. Напишите формулу числа 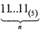, где «л» обозначает любое

количество единиц в числе.

Исп. 1 000 = 125 = 5³; 10 000 = 625 = 5⁴;

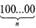= 5-'.

Так здесь почти то же самое, что и в десятичной системе. 11...1L.-, =5"~'+5"-²+...+,..

А как же в конце? 11 = 6, но это же 5¹ и 1... Правильно: 10=5'

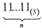
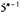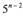+ +... + 5+1.

Эксп. Напишите формулу числа

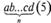I.

Исп. Это уже нетрудно. Так же, как и в десятичной системе, только вместо 10 здесь 5.

Странно, как же это я сразу не использовал формулу, которую нашел для десятичной системы.

Протокол от 4. 01.1957 г.

Эксп. Вчера Вы научились выражать числа в пятеричной системе. Кроме пятеричной системы существуют также другие системы счисления. Например, в четверичной системе счисления числа обозначаются с помощью цифр 1, 2, 3, 0. Найдите число 12324-

Исп. Это уже совсем нетрудно. Общая формула та же, только основание другое. Здесь будет такая формула:

_а 4-4-ft 4»-² +...+ _c-4 + d; 1 232 = 1х 4³+ 2 х 4² + 12 + 2 = 64 + 32 + 12 + 2 = 110

Эксп. Данатринадцатеричная система (1, 2, 3,4, 5,6, 7, 8,9, т, к, I, о). Найдите число

Исп. Теперь я могу находить в любой системе. Формула здесь будет такая:

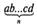(l3) = fl-13"-' + 6-13"-² +... + c-13 + rf.

Только посмотрим начальные числа... 10 = 13,12 = 15... 13 + 2 = 15, правильно. Возьмем 23. Это 13 + 10 = 23. Так же, как и раньше...

\tnlo = 1 • 13³ + 10 ■ У + 12 ■ 13 + 0 = 2 197 + 1 690 + 156 = 4 043.

Эксп. Напишите формулу числа в любой позиционной системе счисления

где «к» — любое основание системы 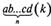счисления. Исп. Это ясно само собой:

a-k^nl + b-k"-²+... + c-k+d.

Приведенный протокол дает возможность проследить как процесс выделения закономерности, составляющей принцип построения числа в десятичной системе, так и роль этого принципа в дальнейшем анализе при выполнении задания: выражать числа в пятеричной системе счисления.

Испытуемые умеют писать числа в десятичной системе и знают основные способы действия с этими числами, но не могут выполнить задания — написать формулу образования числа. Как мы видели в протоколе, выполнение этого задания требует анализа отношений, составляющих принцип построения числа. От испытуемого требуется написание любого числа, т. е. его формулы, для чего указаны все необходимые элементы числа: основание системы и число цифр. Однако для того, чтобы использовать эти элементы, испытуемый должен выделить их значение в построении числа. Показатель «я», обозначающий число

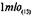
членов числа, может быть использован в построении числа только тогда, когда испытуемый выделит роль места цифры в числе, что определяется именно количеством цифр числа. Но и этого еще недостаточно. Только анализ образования разрядов числа на основе выделения основания системы счисления позволяет соотнести способ образования разряда со способом выражения разряда, т. е. найти подлинное значение «л».

Испытуемый не знает значения каждого элемента формулы числа, поэтому он и «не может понять», как написать формулу числа. Испытуемый выделяет значение числа цифр («и»), но при этом цифры числа не осознаются как показатели разрядов.

Поэтому, ставя перед испытуемым следующую задачу (найти формулу числа 100...00), мы оставляем лишь одну

т

задачу — раскрыть отношения между местом цифры в числе (выраженным любым количеством нулей — «т») и основанием системы. Но оказывается, что для испытуемого и эта задача «не легче». Вся трудность заключается в том, что «нулей» может быть любое число. И это — реальная трудность, преодоление которой требует специального анализа. Число с определенным количеством нулей может написать каждый, формула же требует выразить любое число другим способом, в котором содержание разряда вы -ражалось бы не непосредственно количеством нулей, а некоторым отношением, выражающим способ образования разряда. Предлагая испытуемому решить эту задачу для случая, где т — 5; мы не снимаем этой трудности, а лишь даем испытуемому реальное число, которое содержит определенное количество нулей. Это позволяет испытуемому соотнести конкретное число с требованиями задачи — найти значение «т», т. е. предоставляет испытуемому возможность проанализировать число в соответствии с требованием задачи — найти формулу числа при любом количестве нулей. Испытуемый может написать число при «/и», равном 5 (100 000), но задача требует найти формулу этого числа, в которой количество нулей, поставленных после единицы, было бы заменено соотношением 10⁵. Требования задачи направляют процесс анализа числа, соотнесение ряда чисел, имеющих различное количество нулей: «Значит, пять нулей — 100 000... Ага, посмотрим — 10,

;28

100... Так... Когда я прибавлю один нуль, тогда число увеличивается в 10 раз. Здесь будет 10⁵, а 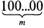= 10^т.

Выделяемое испытуемым отношение между соседними разрядами («больше в десять раз») принадлежит к числовому содержанию, но в соответствии с требованиями задачи оно соотносится испытуемым с формой обозначения числа, где это отношение выражается различным количеством нулей.

Соотнесение чисел с количеством нулей, различающимся на единицу, позволяет испытуемому проникнуть в отношения, которые составляют содержание числа, и установить зависимость между формой числа и его содержанием.

В результате этого соотнесения испытуемый выделяет значение 10 как основание степени и значение «т» как его показатель. Это есть основное отношение, составляющее принцип образования единицы любого разряда как отдельного числа. Но, выделив этот принцип, испытуемый не может написать формулы числа, в котором каждый разряд обозначен с помощью единицы. Здесь уже нет нулей, определяющих содержание единицы разряда в зависимости от его места. Место единицы в числе определяется наличием других единиц, обозначающих разряды. В данном случае нужно найти второй (аддитивный) принцип образования числа в десятичной системе — с помощью сложения разрядов, заключенных в числе.

Соотнося новую задачу с только что решенной, испытуемый в решении новой задачи первоначально пытается использовать найденный им способ выделения принципа построения разряда путем соотнесения соседних разрядов: «Но с единицами так не пойдет. Возьмем 11, 111, 1111... Какая же здесь соблюдается последовательность? Никакой последовательности не вижу. Как же здесь разобрать?»

В предыдущей задаче каждый разряд представляет собой отдельное число. В новой задаче от испытуемого также требуется написать формулу образования числа, но состоящего из различных разрядов. Испытуемый не выделяет этого внутреннего различия чисел, поэтому он и соотносит их недифференцированное числовое содержание на разряды.

Поставленная перед испытуемым задача требует анализа внутренних отношений в числе, требует выделения разрядов, из которых состоит число. Естественно, что такой

анализ можно произвести только на конкретном числе: неизвестное, выраженное в требованиях задачи, может лишь направлять этот процесс анализа. Поэтому задача найти содержание каждой единицы в числе требует расчленить число, разложить его на разряды, образование которых известно. Это позволяет испытуемому перейти к более глубокому анализу числа, определяемому требованием — написать его формулу. Испытуемый находит формулу построения числа, в котором каждый разряд обозначен единицей, выделяя отношения между разрядами внутри числа.

Решая следующую задачу, которая включает различные показатели разрядов в числе, испытуемый использует для анализа как ранее выделенные отношения, составляющие принцип построения числа, так и способ анализа, выраженный в соотнесении неизвестного «любого» числа ab...cd с конкретным числом, в котором п = 4.

п

В процессе соотнесения испытуемый разлагает неизвестное «любое» число при п = 4 на его разряды, показателями которых теперь являются буквы а, Ь, с и d. На основе этого опосредования, представляющего собой разложение числа, произведенного в решении предыдущей задачи, испытуемый находит общую формулу любого числа в десятичной системе.

Мы видим, таким образом, что нахождение формулы числа в десятичной системе является результатом анализа и синтеза, последовательно раскрывающих закономерные отношения в числе. Решая поставленные задачи, испытуемый выделил позиционный принцип построения числа в десятичной системе, выразил эти закономерные отношения в общей формуле и использовал их для обозначения конкретного числа.

После того, как испытуемый вычленил закономерность построения числа в десятичной системе счисления, ему было предложено обозначить число 17 в пятеричной системе счисления с помощью цифр 1, 2, 3, 4, 0. Как мы уже указывали, нас интересовала роль, которую будет играть выделенная испытуемым закономерность в процессе усвоения новой системы счисления, основанной на том же самом (позиционном) принципе.

Как видно из протокола, выполняя задание (обозначить число 17), испытуемый в условиях новой задачи не

может выделить тех закономерностей, которые им были раскрыты для десятичной системы счисления, поэтому он и не может сразу найти способ обозначения числа в новых условиях. Несоответствие старого способа новым условиям вызывает процесс анализа условий задачи: «Здесь должна быть какая-то система, какой-то принцип. Если я напишу так же, как в десятичной системе, например, один и два (12), то это будет двенадцать?.. А зачем здесь дан нуль? Ведь 4 и 0 — это все равно не будет сорок. «0» в десятичной системе показывает место цифры, а здесь он зачем?»

Анализируя новые условия, испытуемый соотносит как числа, выраженные с помощью цифр пятеричной системы (22), так и отдельные ее элементы (например, количество цифр) с соответствующими числами (12) и элементами десятичной системы. Но, как видно из протокола, соотнесение с десятичной системой не ведет к какому-либо продуктивному результату. Испытуемый устанавливает лишь различие систем счисления с различным основанием, не раскрывая общего принципа обозначения чисел в различных позиционных системах. «Ведь это отдельные цифры, которые не имеют никакой системы», — заявляет испытуемый, не обнаруживая здесь закономерности, на основе которой строится число в десятичной системе. Испытуемый не видит того, что здесь нужно использовать общую закономерность, заключенную в десятичной системе.

Задание написать число 17 в пятеричной системе может быть выполнено сразу, лишь когда уже выделена общая закономерность построения чисел в этой системе. Испытуемый не выполняет этого задания, поэтому мы ставим перед ним более простое задание — написать число 5. Это задание может быть выполнено без помощи общей формулы путем продолжения числового ряда. Для числа 5 нет соответствующей цифры в пятеричной системе, его нужно обозначить другим способом. Потребность в способе обозначения числа вызывает процесс анализа, который, как мы видим из протокола, осуществляется и здесь через акт синтеза. Этот синтез выражается в соотнесении числа, требующего своего обозначения, с соответствующим ему (по месту, занимаемому в числовом ряду) по форме числом десятичной системы. Испытуемый говорит: «Здесь, когда дальше нет цифр, должен начинаться второй ряд: 1, 2, 3. 4, 0; 1, 2, 3, 4, 0... Это второй ряд. Посмотрим, как обозначается вторая единица в десятичной системе? Там единица

и нуль — это десять. Выходит, что здесь единица с нулем — это будет 5... Когда я пишу 1 — это 1. Когда один с нулем — это 10. Здесь, когда 1 — это 1. В десятичной дальше две единицы (11) — это 11. А здесь тогда 11 — это — 6... Вот и все. Я строю по десятичной системе... 21 = 11, 22 = 12...»

Опираясь на соотнесение получающегося таким образом числового ряда пятеричной системы с соответствующими элементами ряда десятичной системы, испытуемый выделяет форму обозначения числа в пятеричной системе и находит соответствующий выделенным отношениям способ обозначения.

Но этот способ не основан на выделении закономерности построения числа в пятеричной системе счисления, поэтому испытуемый продолжает анализ с целью выделения закономерности, необходимой для выполнения поставленного задания:

Эксп. Напишите 38 (в пятеричной системе).

Исп. Здесь нужно найти систему, а то Вы, пожалуй, дадите написать какое-либо большое число... 5 = 10; 10 = 20; в два раза больше. А24= 14; 32 = 17... Нет, системы я еще не знаю.

Необходимость анализа новых условий определяется потребностью в выделении общей закономерности. Для этого испытуемый строит числовой ряд в пятеричной системе счисления:

1 2 3 4 10 11... 12 3 4 5 6

и т. д. (См. решение испытуемым Л. Д. задачи написать число 149 в пятеричной системе, с. 125—126).

Анализируя числовой ряд, испытуемый выделяет «основные числа» («Возьмем основные числа: 5,25... Дальше должно быть 125и так далее... Это 5 в какой-то степени»), составляющие единицы разрядов усваиваемой новой системы счисления. Соотнося их друг с другом, испытуемый выделяет принцип образования разрядов в новой системе счисления, выделяет основание системы счисления (5) как основную единицу образования числа в пятеричной системе счисления. На основе его выделения испытуемый действительно может найти любое число, хотя он и не раскрыл еще других отношений, составляющих закономерность, выражаемую в формуле числа. Для того чтобы

найти формулу числа, недостаточно знать принцип образования разрядов. Нужно еще раскрыть способ соединения различных разрядов в числе, форму их выражения не как отдельных чисел, а как таких единиц счета, из которых состоит любое число.

Поэтому мы далее предлагали испытуемому задачу (найти число 111(5) которая требовала анализа этих отношений, необходимых для выделения выражаемой в формуле закономерности (см. Протокол № 30: с. 124).

Разлагая число пятеричной системы на составляющие его разряды, испытуемый находит числовое содержание новых разрядов. При этом он использует для анализа ранее выделенный принцип образования разрядов. На этой основе испытуемый выделяет аддитивный принцип образования числа, форму выражения разрядов не как отдельных чисел, а как компонентов числа.

Таким образом, основные отношения, составляющие закономерность образования числа в пятеричной системе счисления, выделены испытуемым до решения задачи, требующей найти формулу числа при решении задачи обозначить число в пятеричной системе. Задача «написать формулу числа» решается испытуемым сразу потому, что им уже выделены те отношения, которые теперь нужно выразить и формуле числа.

Необходимость в выделении закономерных отношений в формировании обобщения определяется здесь тем, что вне обобщения испытуемый не смог бы выполнить предлагаемого ему задания.

В качестве контрольного эксперимента, в котором можно было проверить уровень обобщения и его роль при выполнении задания в новых условиях, мы ставили перед испытуемым задания, требующие обозначать числа в двух (новых) позиционных системах счисления и найти формулу построения числа для любой позиционной системы счисления.

Как показывает приведенный протокол, выделение закономерности построения числа в пятеричной системе счисления позволяет испытуемому использовать эту закономерность для обозначения числа в условиях других позиционных систем счисления. Испытуемый теперь уже не анализирует принципов построения числа в новых условиях, а использует ранее найденную формулу, учитывая те изменения, которые произошли в условиях задания: «Общая

формула та же, — говорит испытуемый, — только основание системы другое». Испытуемый может теперь написать также формулу числа для любой системы счисления.

Это значит, что в процессе усвоения пятеричной системы счисления испытуемый раскрыл закономерные отношения, составляющие содержание обобщения. Наличие обобщения и позволило испытуемому действовать в новых условиях без их предварительного анализа.

В чем же заключаются причины того, что испытуемый не может использовать раскрытой им закономерности после ее выделения в условиях десятичной системы и, напротив, использует ее на основе анализа условий обозначения в пятеричной системе?

Объяснение этого факта мы видим в характере тех этапов, которые проходит процесс анализа до достижения требуемого обобщения.

Анализируя условия обозначения в десятичной системе счисления, испытуемый выделяет лишь отношения, необходимые для выполнения задания в данных конкретных условиях. Раскрываемая испытуемым закономерность оказывается слитой с теми конкретными отношениями, которые составляют принцип построения числа в десятичной системе. И, пытаясь использовать найденную им формулу целиком, а не ее общей принцип, испытуемый естественно приходит к выводу о невозможности выполнения задания в новых условиях в соответствии с закономерностями десятичной системы.

Для выполнения задания в новых условиях требуется более высокий уровень обобщения, содержанием которого является закономерность построения любого числа в любой позиционной системе счисления. Путь выделения этой общей закономерности, составляющей новый уровень обобщения, и выражен в процессе анализа пятеричной системы счисления. Раскрывая закономерности обозначения числа в пятеричной системе, испытуемый проходит ряд этапов, характеризующих движение процесса анализа и достигаемые при этом различные уровни обобщения.

1. На первом этапе анализа условий обозначения в новой системе счисления испытуемый, соотнося условия обозначения чисел в новой системе с их обозначением в десятичной системе, раскрывает формулу обозначения отдельного числа. На этой основе он может обозначать

числа только путем продолжения числового ряда от известного числа (5 = 10; 6 = 11; 7 = 12 и т. д.).

2. На втором этапе, выделяя в полученном числовом ряду единицы разрядов новой системы счисления (5, 25, 125) и соотнося их, испытуемый раскрывает принцип образования единиц разрядов. На основе выделения этой закономерности испытуемый может обозначать числа путем продолжения числового ряда по единицам разрядов (25=100; 125=1 000; 625=10 000; 627=10 002), не используя всего числового ряда.

3. На третьем этапе, разлагая число, обозначенное с помощью единиц (111 = 125 + 5 + 1 = 131), испытуемый раскрывает принцип соединения различных разрядов в числе. Это позволяет ему обозначать числа, разлагая их на единицы разрядов и не используя при этом числового ряда (627 = 10 000 + 2 = 10 002).

4. Используя результаты проделанного анализа, испытуемый на четвертом этапе без труда раскрывает формулу построения любого числа в новой системе счисления. На этой основе он может сразу как обозначить любое число в новой системе счисления, так и найти числовое содержание, выраженное в новой форме (1 023 = 125 + 10 + 3=138).

5. Соотнося далее закономерность построения числа в пятеричной системе с закономерностью построения числа в десятичной системе, испытуемый дифференцирует различия в основаниях систем счисления и выделяет общее значение основных отношений для обозначения числа в различных позиционных системах. Это и позволяет испытуемому после анализа условий обозначения числа в пятеричной системе обозначать числа в любых позиционных системах счисления.

Этапы движения процесса анализа и достигаемые при этом различные уровни обобщения позволяют объяснить факт использования раскрытой испытуемым закономерности в новых условиях в результате анализа условий обозначения пятеричной системы счисления. Однако этапы движения процесса анализа не позволяют полностью объяснить второй факт — отсутствие такого использования после выделения закономерности в условиях одной десятичной системы. С целью объяснения этого факта были проведены еще две серии экспериментов (вторая и третья).

Обобщение отношений на основе

предварительного обозначения чисел

в пятеричной системе

Во второй серии экспериментов перед испытуемым вначале ставилось задание обозначать числа в пятеричной системе счисления. Так как попытки испытуемого выполнить это задание не приводили к успеху, мы ставили перед ним задачу рассмотреть образование числа в десятичной системе. После того как испытуемый находил формулу образования числа десятичной системы, мы возвращали его к решению первой задачи.

Рассмотрим результаты экспериментов.

Протокол №35 от 9.01.1957г. Исп. Г. А.

Эксп. В школе Вы учили десятичную систему счисления. Для обозначения любого числа в десятичной системе мы пользуемся десятью цифрами 1,2,3...8,9,0. Кроме десятичной системы счисления есть другие системы счисления. В пятеричной системе счисления для обозначения любого числа достаточно пяти цифр: 1, 2, 3, 4, 0. Ваша задача заключается и в том, чтобы писать числа в пятеричной системе счисления. Напишите число 17.

Исп. Так... Допустим, что 17- 1034(10= 10; 3 = 3; 4 = 4; 10 + 3 + 4= 17.- А. М.)... Но только как тогда построить другие числа?.. Нет, такое вряд ли подойдет... 5,6,7,8,9... Получается, что десять уже есть, а 9,8 и другие числа обозначить нельзя. Если тогда сделать 01, 02, 03, 04: 01 — это 5, 02 — шесть. Но тогда получается, что 32 тоже равно 5 (путем сложения. —A.M.), 41 также 5. Это неоднозначно, так нельзя. А можно ли здесь складывать или умножать?

Эксп. Нет, нельзя.

Исп. Я сейчас посмотрю, как строятся числа в десятичной системе... 1,2, 3,4, 5, 6, 7, 8,9, 0... Но я не знаю, что выбрать за эти числа (6,7, 8, 9). Ведь нужно сделать так, чтобы обозначения были однозначны.

Эксп. А Вы хорошенько рассмотрите, как образуются числа в десятичной системе.

Исп. Здесь-то просто: присоединяется цифра и получается новый разряд... 10 = 10,11 = 11 итак далее. Так, нужно извлечь такой метод, который можно было бы перенести и в пятеричную систему. Мне вот понятно, как в начале... (образуются числа в десятичной системе. — А. М.), а как будет дальше, не знаю. 5—10,11—6,12—7,13—8,14—9... Как же дальше? Пусть будет так: 20-10, 21- 11, 22-12,23-13, 24-14, 25-15...

Эксп. Пяти нет.

Исп. 20.10 будет 15, а 17 тогда будет 20.12.

Эксп. Но ведь так складывать нельзя.

Исп. Как же по-другому? Если, например, 30 = 20, то тогда не будет семнадцати, восемнадцати.

Эксп. Продолжим анализ десятичной системы. Напишите формулу образования числа в десятичной системе, если

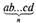(10)

любое число, в котором буквы являются любыми цифрами, а «я» указывает на любое их количество в числе.

Исп. Какая же здесь может быть формула построения? Не понимаю.

Эксп. Возьмем другую задачу. Дано число десятичной системы

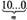
в котором «т» обозначает любое количество нулей. Как оно образовано?

Исп. Если число нулей указано, значит ясно, какое число. Например, три нуля — это тысячи.

Эксп. Даны 9,4,5. Напишите все различные числа, состоящие из этих цифр.

Исп. 945, 954, 495, 459, 594, 549.

Эксп. Напишпте, что обозначает каждая цифра в этих числах.

Исп. Это значит: 945 = 900 + 40 + 5; 954 = 900 + 50 + 4; 495 = 400 + 90 + 5. Здесь место цифры и сама цифра дают какое-то число. Но опять не только это. В десятичной системе в зависимости от места цифры мы имеем то или иное (ее) значение... Первое место — единицы, второе место — десятки, третье место — сотни...

Эксп. Напишите формулу числа

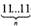(10)

Исп. 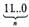(10)= 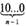+ +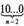...+ 10+1.

Эксп. Напишите формулу числа

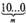, если т = 1 221.

Исп. Это число, в котором количество нулей 1 221. Такие большие числа еще обозначают так: 10¹²²¹.

Эксп. Почему?

Исп. Потому что здесь существует равенство, например, 100=10². Тогда числоможно записать как 10™, а

будет равно 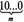10"-' + Ю"² +..'..+ 10 + 1.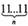

Эксп. Продолжим решение задачи в пятеричной системе. Нам нужно было обозначить 17.

Исп. Я обозначил 17 как 20.12, но здесь я использовал различные способы обозначения, один вначале (11 = 6) и второй теперь (20.11 = 16). Нужен какой-то один. Я очень привык к десятичной системе, и это мешает. Допустим, мне нужно записать 196. Как же я его запишу? 10—5; 20—10; 30-15. Нет, 30 не будет 15. Ачтоже будет 30? 20.14-19, 30-20.

Эксп. Вы обозначаете различными способами.

Исп. В десятичной системе хорошо, там четкий закон построения числа, а здесь? Здесь... Ну, хорошо... Я боюсь запутаться в этих числах, поэтому возьму по-другому... 10—5; 20—6; 30—7; 40—8, но так не получается 9. Если взять, например, двоичную систему, то там наверное будут две цифры: 1 и 0. Здесь какое-то особое значение имеет 0. Но я этого не могу понять.

Эксп. Вы все-таки напишите 17.

Исп. Я все хочу найти закон.

Эксп. Но нам нужно писать числа. Вы написали 14, продолжайте дальше.

Исп. Сейчас соображу... Так, 210 = 15, 211 = 16, 212 = 17. Так а если нужно записать 190, как же здесь записать 90? Кажется, что это неудачный способ.

Эксп. 10 Вы выражали как 20, а теперь выражаете как 200.

Исп. Да, это не годится. Я могу, пожалуй, поставить 30 = 15, тогда 31 = 16, 32 = 17. Дальше, очевидно, 40 = 20, 50 = 50, 60 = 30.

ьЭксп. Нет таких цифр (5,6).

Исп. 40 = 20... А как же записать 100?

Эксп. Напишите 28.

Исп. Я хочу написать сразу 196, а потом 28. В десятичной системе 12 это 10 + 2. На втором место десятки, на третьем — сотни. Знак «+» можно подразумевать также и через две цифры. Число десятков тоже через две цифры: 00-0; 01-1; 02-2; 03-3; 04-4... 10-5; 11-6; 12-7; 13-8; 14—9...Тогда 190 запишется так: 01 14 11. Я нашел все цифры и использовал принцип десятичной системы.

Эксп. В условии задачи Вам были даны цифры 1 = 1; 2 = 2; 3 = 3; 4 = 4. Это их значения. Искать их не нужно, а с их помощью нужно обозначать другие числа.

Исп. Значит, все-таки нужно писать в пятеричной системе. Но я ее не знаю. Если бы я знал закон, тогда было бы просто. А если использовать римскую нумерацию?

Эксп. Данных цифр менять нельзя. Напишите числовой ряд до 28.

Исп. До 28, пожалуй, можно, но 90 тогда опять вряд ли получится.

Эксп. Все-таки напишите 28.

Исп. 20 = 10; 30 = 15; 32 = 17; 33 будет 18; 34 = 19; 40 = 20; допустим, что 43 будет 28.

Эксп. Почему?

Исп. Да, а как тогда будет 21?

Как же тут разобраться? Если 40.10—21, то это не годится. Я буду вновь записывать числа... 31—16; 34—19; 40—20, а 41 что будет значить? 41 — это 21... Хорошо, тогда 44—24; 50—25. Нет, так нельзя. Как же записать 25? 40—20 и 10—5, если 40.10, то это не получается. Здесь как бы два различных ряда. Цифры, первые справа, обозначают самих себя, (единицы. — Л. М.), а вторые зависят от тех, которые перед ними. Здесь получается какая-то сложная зависимость... 44 это 24. Дальше придется писать на третьем месте. Допустим, я нахожу 110. Тогда противоречие. Нужно найти какой-то общий закон, тогда уже писать. Если 101 = 11,300 = 30, то 50 обозначить нельзя.

Эксп. А нет ли в десятичной системе таких случаев, когда число составлено из самых больших значений цифр?

Исп. Есть, это 99, затем следует 100. Тогда здесь также 25—100. Как тогда 26? Это 101, а28—103; 29-104. Но 30? Как же тогда 30?Так, 29-104. 30-110; 31-111; 32-112; 33-113; 34-114; 35... Придется так: 35-120... 39-124; 40 - это 130; 44-134; 45-140... Дальше 150, нельзя... 141-46; 144—49; 50... Придется ставить следующее 50—200. Теперь вотя начинаю немного чувствовать... 100-25, 200-50; 300-75,400-100.

Эксп. Напишите 136.

Исп. Какой же все-таки здесь закон? Буду продолжать... 401—101; 404-104; 410-105; 414-109; 420-110; 424-114; 430-115; 434-119; 440-120; 444-124... 1 000-125... Тогда 1 004-129; 1 010-130; 1 014-134; 1 020-135; 1 024-139; 1 030-140; 1 034-144; 1 040-145; 1 044-149;

1 100-150; 1 104-154; 1 110-155; 1 120-160; 1 140-170; 1 144-174; 1 200-175; 1 300-200.

Эксп. Найдите число 11 111₅. Продолжать числовой ряд нельзя.

Исп. Тогда мне остается только находить значение чисел, которые составляют 11 111. Мне собственно нужно найти 10 000... 10 = 5, 100 = 25,

I 000 = 125... Но как же 10 000? Ага, да здесь совсем неплохо... 5 • 5 = 25; 5-5 • 5 = 125. Получается, что каждое новое число увеличивается в пять раз, тогда 10 000 = 125 • 5 = 625,11111 = 781.

Эксп. Найдите 100 000.

Исп. 100 000 = 625x5 = 3 125.

Эксп. Найдите формулу числа

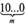(5)-

Исп. Так 10—5; 100—5², здесь тогда будет

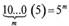
Эксп. Найдите формулу числа

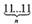(5)

Исп. Сейчас будем соображать... 1—1; 11—6; 111—31; 1 111—156;

II 111—781... Ничего так не получается. Хотя... Стоп, нужно рассмот-реть каждое число. 11 = 6 = 5+1; 111 = 25 + 5+ 1; 1 111 = 156=125 + 5+1; 11 111 = 625 + 125 + 25 + 5 + 1 = 781, Ага, закон открыт. Здесь 11 111 = 5⁴+ +5³+5²+5+1.

Эксп. Напишите формулу числа

q^cd(5).

л

Исп. Так, а с этим не скоро разберешься. А если взять двойку: 2—2; 22-12; 222-? 100-25; 112-32; 200-50... Не совсем понятно. А есть здесь какой-нибудь закон?

Эксп. Найдите число 4 231₍₅), не пользуясь таблицей.

Исп. Я знаю, что обозначает 1 000; но не знаю, что обозначает 4 000. Меня так и тянет построить таблицу (числового ряда — А. М), чтобы найти 4 000.

Эксп. Строить таблицу нельзя.

Исп. Без этого трудно, нужно руководствоваться каким-то принципом. Что, например, здесь означает четверка..? Когда единица, тогда ясно (1 000. — А. Л/.), а если 4 000? Придется все-таки составлять таблицу, по-другому я не могу... 1 000-125; 1 100-150; 1 200-175.

Эксп. Найдите без таблицы чему равняется 400.

Исп. 100 = 25, а 200 что это?. Что 50, в два раза больше... 300—75; 400-100... Это 4 х 25. Понятно, 4000 = 125 х 4 = 500.

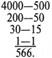
Теперь я могу найти формулу числа... 4 000 это 4 по 1 000,1 000 — это 5 в третьей степени

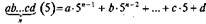
Эксп. Найдите число 32 320(5).

Исп. Теперь я могу находить любое число... 32 320₍₅)= 3-5⁴ + 2-5³ + 3-5² + + 2-5 + 0 = 3-625 + 2- 125 + 3-25 + 10 = 187 + 250 + 75 + 10 = 2 210

Протокол от 10. 01.1957 г.

Эксп. Теперь мы с Вами будем считать в троичной системе счисления, где для обозначения любого числа достаточно трех цифр: 1,2,0. Найдите 1 120₃.

Исп. ',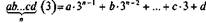

1 120₍,=3³+3²+2-3=27+9+6=42.

Эксп. Найдите число 17₍ю) в троичной системе счисления.

Исп. 17 можно записать как З² + 3 и остается 5. Как представить 5? Нет, даже не так. 17 = З² + 3 х 2 + 2, что будет равно 122.

Эксп. Выразите число 39(Ю) в троичной системе.

Исп. Это пойдет быстро, потому что у меня есть общая формула... 39= З³ + З² + 3 = 111. Странно, почему-то меньше, чем 17. Ясно, здесь же нет единиц... 39= 1 ПО.

Эксп. Дана двенадцатиричная система, в которой, кроме 1, 2... 8, 9, есть еще цифры «а» = 10; «Ь» =11 и 0. Найдите число \аЬ₍п).

Исп. 1 db_m = 1 • 12² + а ■ 12 + Ь = 144 + 120 + 11 = 275.

Эксп. Напишите формулу числа для любой системы счисления (осно -вание системы может быть к).

Исп.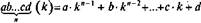

Эксп. Найдите число И 100, записанное в двоичной системе счисления.

Исп. 11 100 =... Но ведь здесь всего один знак (1.— А. М.)... 1 + 1 + 1... Нет, что-то не то. Здесь в основании 2, тогда 11 100= 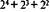=16 + 8 + 4 =

= 28.

Эксп. Найдите число 37₍ю) в двоичной системе.

Исп.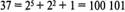

Приведенный протокол показывает, что испытуемый Г. А. не использует выделенной в десятичной системе закономерности построения числа для обозначения числа в пятеричной системе. Получив задание написать число 17 в пятеричной системе счисления, испытуемый анализирует различные известные ему способы образования числа и отбрасывает эти способы как не удовлетворяющие условиям обозначения числа 17 при помощи ограниченного количества цифр. Далее испытуемый, анализируя условия обозначения чисел 6, 7, 8, 9 в соответствии с новыми требованиями, изменяет значение цифр пятеричной системы

путем присоединения к ним нуля. Но так как результат такого обозначения ведет к многозначности в выражении одного и того же числа, что не соответствует требованиям обозначения, то испытуемый начинает новый процесс анализа: «Я сейчас посмотрю, как строятся числа в десятичной системе...».

В процессе анализа способов обозначения числа испытуемый сам обращается к анализу числа в десятичной системе. Поэтому момент включения анализа десятичной системы в процессе анализа пятеричной системы соответствовал переходу испыту