2015-06-05
582
Свободные электромагнитные колебания в контуре. Формула Томпсона.
Пусть конденсатор ёмкостью C заряжен до напряжения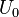 
. Энергия, запасённая в конденсаторе составляет
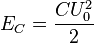
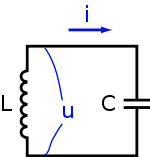
Параллельный колебательный контур
При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток
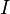, что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора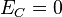 
. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
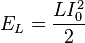, где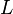 
— индуктивность катушки, 
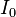— максимальное значение тока.
После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения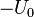 
.
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
В общем, описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.
Напряжение на идеальной катушке индуктивности при изменении протекающего тока:
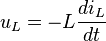
Ток, протекающий через идеальный конденсатор, при изменении напряжения на нём:
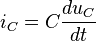
Из правил Кирхгофа, для цепи, составленной из параллельно соединённых конденсатора и катушки следует:
, — для напряжений,
и
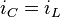— для токов.
Получаем:
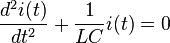
Это дифференциальное уравнение гармонического осциллятора с циклической частотой собственных колебаний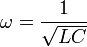 
(она называется собственной частотой гармонического осциллятора).
Решением этого уравнения 2-го порядка является выражение, зависящее от 2 начальных условий:
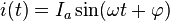
где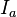 
— некая постоянная, определяемая начальными условиями, называемая амплитудой колебаний, 
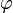— также некоторая постоянная, зависящая от начальных условий, называемая начальной фазой.
Например, при начальных условиях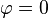 
и амплитуде начального тока 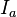решение сведётся к:
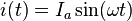
Электромагнитные колебания - колебания электрических и магнитных полей, сопровождаемые изменением заряда, силы тока и напряжения.
