Консервативный гармонический осциллятор

Второй закон Ньютона для такого осциллятора запишется в виде: 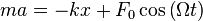. Если ввести обозначения: 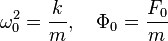и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:

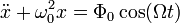
Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:

,

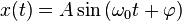где 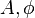— произвольные постоянные, которые определяются из начальных условий.

Найдём частное решение. Для этого подставим в уравнение решение вида: 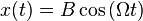и получим значение для константы:

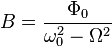
Тогда окончательное решение запишется в виде:

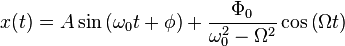
Резонанс

Из решения видно, что при частоте вынуждающей силы, равной частоте свободных колебаний, оно не пригодно — возникаетрезонанс, то есть «неограниченный» линейный рост амплитуды со временем. Из курсаматематического анализаизвестно, что решение в этом случае надо искать в виде: 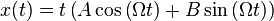. Подставим этотанзацвдифференциальное уравнениеи получим, что:

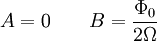
Таким образом, колебания в резонансе будут описываться следующим соотношением:

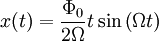
Затухающий гармонический осциллятор

Второй закон Ньютона:

.

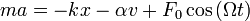Переобозначения:

Дифференциальное уравнение:

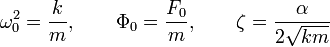
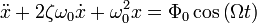
Его решение будет строиться, как сумма решений однородного уравнения и частного решения неоднородного. Получим и проанализируем частное решение.

При подстановке ее в уравнение (5.7) получим уравнение вынужденных колебаний 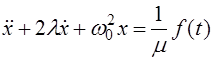(5.23)

Уравнение (5.23) — это уже неоднородное дифференциальное уравнение. Его решение дается суммой общего решения однород­ного уравнения (5.10) и частного решения уравнения (5.23): (5.24)

Наиболее интересным случаем вынужденных колебаний является случай, когда внешняя обобщенная сила представляет собой гар­моническую функцию

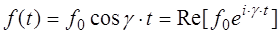(5.25)

Где 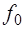— действительная постоянная. Для гармонической выну­ждающей силы уравнение (5.23) удобно записать и решать в ком­плексной форме:

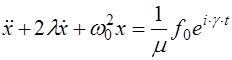(5.26)

В правой части уравнения (5.26) стоит экспонента. Поэтому его частное решение 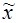также ищем в форме экспоненты 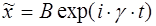. Подставляя 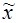в такой форме в уравнение (5.26), находим постоянную :

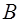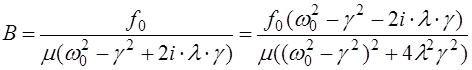(5.27)

Представим постоянную 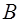В экспоненциальной форм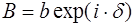е , где

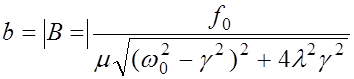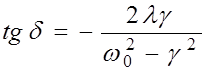; (5.28)

Тогда действительная часть общего решения уравнения(5.23) с гармонической вынуждающей силой (5.25) запишется в виде

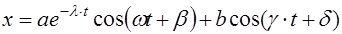(5.29)

В отсутствие трения 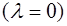вынужденные колебания (5.29) являются суммой свободных колебаний с частотой 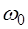и вынужденных колебаний с частотой вынуждающей силы 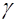И амплитудой, зависящей от частоты:

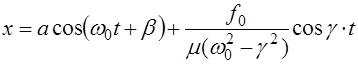(5.30)

Фаза вынужденных колебаний совпадает с фазой вынуждающей силы. Амплитуда вынужденных колебаний растет при 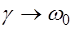. Если 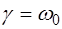, то наступает Резонанс и решение (5.30) не имеет смысла. В этом случае частное решение уравнения (5.26) необхо­димо искать в виде 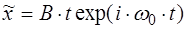Для постоянной 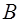Получаем значение 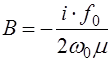(5.31)

Уравнение малых колебаний в случае резонанса принимает вид

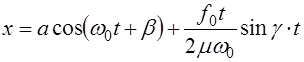*. (5.32)

При резонансе фаза вынужденных колебаний на 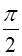отличается от фазы вынуждающей силы. Амплитуда вынужденных колеба­ний монотонно растет с течением времени, и колебания быстро перестают быть малыми.

Рассмотрим поведение системы вблизи резонанса, когда частота вынуждающей силы мало отличается от частоты свободных коле­баний. Положим, что 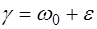, где 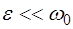. Выражение (5.30), записанное в комплексной форме, можно привести к виду (5.33)

В выражении (5.33) нужно учитывать только действительную часть, которая равна

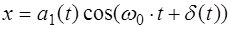, (5.34) где

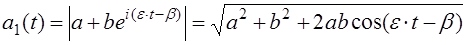(5.35)

Уравнение (5.34) можно интерпретировать как уравнение колеба­ний с часютой 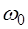, амплитуда 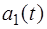и начальная фаза 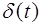которых медленно меняются с частотой 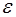. Как видно из (5.35), амплитуда заключена в пределах

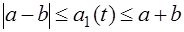(5.36)

Есл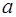и и 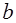близки друг к другу, то временами колебания будут по­чти прекращаться, а после опять возобновляться. Такое поведение системы называют Биениями.

Перейдем к общему случаю, когда присутствует трение 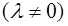При наличии трения первое слагаемое в (5.29) быстро обращается в нуль за счет экспоненциального множителя. В установившемся режиме остается только второе слагаемое. Вынужденные коле­бания происходят с частотой вынуждающей силы, но отстают от нее по фазе. Начальная фаза вынужденных колебаний, как вид­но из (5.27) и (5.28), лежит в пределах 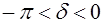. При силь­ном трении, когда 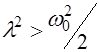, амплитуда вынужденных колебаний монотонно убывает с ростом частоты вынуждающей силы. Если трение мало, то амплитуда максимальна при резонансной частоте .

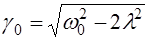Рассмотрим отдельно случай, когда трение очень мало: 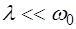. Тогда в первом приближении по 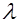резонансная частота 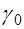Совпада­ет с частотой 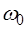. Вблизи резонанса положим 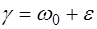,где 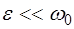. В первом приближении по 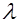и 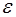Для амплитуды и начальной фазы вынужденных колебаний получим

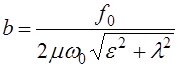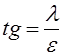; (5.37)

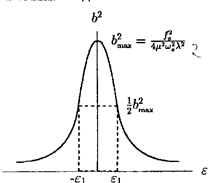
При резонансе, как и в отсутствие трения, колебания отстают от вынуждающей силы на 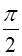. Однако амплитуда остается при этом ограниченной. Как было показано ранее, энергия колебаний про­порциональна квадрату амплитуды. График квадрата амплитуды в зависимости от 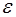приведен на рис. 5.1. Это — типичная ре­зонансная кривая. Если обозначить через 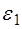Частоту, для кото­рой квадрат амплитуды уменьшается в два раза, то находим, что 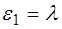. Для характеристики систем, совершающих вынужденные колебания, вводится понятие добротности. Добротность — это отношение максимальной амплитуды для резонансной частоты к амплитуде, отвечающей близкой к нулю частоте вынуждающей си­лы. Используя выражение (5.28) для амплитуды и считая 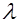малой величиной, найдем для добротности 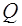значение:

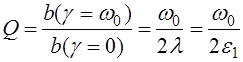(5.38)

То есть чем выше добротность, тем меньше полуширина 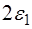резонансной кривой и тем выше поднимается ее пик.