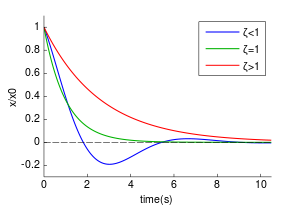
Зависимость графиков колебаний от значения 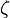 .
.
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
· Апериодичность
Если 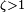 , то имеется два действительных корня, и решение дифференциального уравнения принимает вид:
, то имеется два действительных корня, и решение дифференциального уравнения принимает вид:
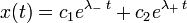
В этом случае колебания с самого начала экспоненциально затухают.
· Граница апериодичности
Если 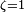 , два действительных корня совпадают
, два действительных корня совпадают 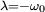 , и решением уравнения является:
, и решением уравнения является:
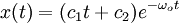
В данном случае может иметь место временный рост, но потом — экспоненциальное затухание.
· Слабое затухание
Если 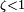 , то решением характеристического уравнения являются два комплексно сопряжённых корня
, то решением характеристического уравнения являются два комплексно сопряжённых корня
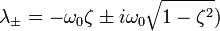
Тогда решением исходного дифференциального уравнения является
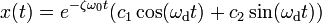
Где 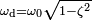 — собственная частота затухающих колебаний.
— собственная частота затухающих колебаний.
По другим источникам 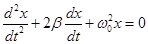 - дифференциальное уравнение затухающих колебаний.
- дифференциальное уравнение затухающих колебаний.
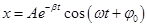 - уравнение затухающих колебаний. (не единственное решение).
- уравнение затухающих колебаний. (не единственное решение).
ω – частота затухающих колебаний: 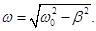 Период затухающих колебаний:
Период затухающих колебаний: 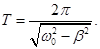
Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз
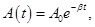
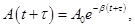
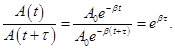
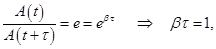
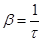
τ - время релаксации.
Коэффициент затухания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент затухания D, который равен отношению амплитуд, отстоящих по времени на период:
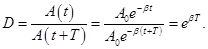
Логарифмический декремент затухания равен логарифму D:
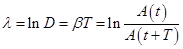
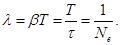
Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания - постоянная для данной системы величина.
Логарифмический декремент колебаний — безразмерная физическая величина, описывающая уменьшениеамплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины в одну и ту же сторону:
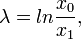
Логарифмический декремент колебаний равен коэффициенту затухания, умноженному на период колебаний:
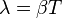
Еще одной характеристикой колебательной система является добротность Q.
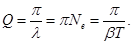
Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.
Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.
Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
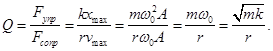
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.
Добротность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Общая формула для добротности любой колебательной системы:
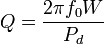 ,
,
где:
· 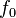 — резонансная частота колебаний
— резонансная частота колебаний
· 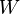 — энергия, запасённая в колебательной системе
— энергия, запасённая в колебательной системе
· 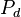 — рассеиваемая мощность.
— рассеиваемая мощность.
Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.
Для последовательного колебательного контура в RLC цепях, в котором все три элемента включены последовательно:
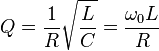 ,
,
где 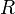 ,
, 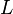 и
и 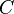 — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.
— сопротивление, индуктивность и ёмкость резонансной цепи, соответственно. 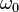 — частота резонанса.
— частота резонанса.
Выражение 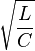 часто называют характеристическим или волновым сопротивлением колебательного контура. Таким образом иное определение добротности - отношение волнового сопротивления к активному.
часто называют характеристическим или волновым сопротивлением колебательного контура. Таким образом иное определение добротности - отношение волнового сопротивления к активному.
Для параллельного контура, в котором индуктивность, ёмкость и сопротивление включены параллельно:
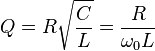 ,
,
В данном случае 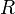 является входным сопротивлением параллельного контура.
является входным сопротивлением параллельного контура.
 2015-06-05
2015-06-05 982
982








