Аналіз за допомогою функції «ЛИНЕЙН»

За допомогою ПП «ЛИНЕЙН» можна отримати оцінки параметрів рівняння регресії 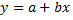, а також його характеристику.

Послідовність роботи:

1) Введіть початкові дані (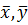) або відповідний файл.

2) Виділити в зручному місці область не зайнятих комірок розміром 5×2 (5 рядків, 2 стовпця) для виводу результатів регресійної статистики або 1×2 – тільки для оцінок параметрів регресійного рівняння.

3) Активізувати майстер функцій: натиснути на панелі інструментів «Вставить функцию» (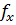) або “Формулы» → «Вставить функцию».

4) В віконці «Мастер функцій» в віконці «Категории» серед «Статистические» вибрати функцію «Линейн» →ОК. При цьому в лівому верхньому куті з’явиться надпис «Линейн ()».

5) В віконці «Аргументы функций» ввести масиви чисел Х – незалежних змінних, У – відповідні незалежні змінні, «Конст» – «1», якщо в рівнянні регресії є стала величина («а»), або «0» – регресійне рівняння рівняння має вигляд 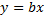; «Статистика» – «1», якщо виводимо всю інформацію (10 комірок), або «0» – тільки значення оцінок параметрів → ОК.

6) В лівій верхній комірці замість «Линейн ()» з’явиться число (оцінка параметра «а». потім необхідно натиснути F2, в лівій верхній комірці з’явиться надпис «Линейн (××:××,++:++,!,?)», де ××:×× – адреса масиву У; ++:++ – адреса масиву Х;! – значення «Конст» («1» або «0»);? – значення «Статистики» ((«1» або «0»).

7) Утримуючи клавіші «Ctrl» та «Shift» натиснути «Enter». після чого всі 10 (або 2) комірки будуть заповнені відповідно оцінки параметрів рівняння регресії (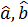); стандартні похибки 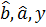; значення коефіцієнта детермінації 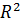; фактичні значення статистики Фішера 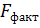; кількість ступенів свободи df; регресійна суму квадратів 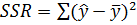; залишкова (непояснювальна за допомогою регресії) сума квадратів .

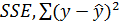8) Дана інформація може бути виражена у вигляді таблиці:

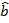
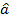
mb	ma
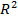
	Wy
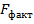
	df

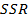
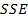
9) Для аналізу регресійних рівнянь, що задані показниковою (експоненціальною) функцією використовують функцію «ЛГРФПРИБЛ» за алгоритмом, який опи

[1] Точніше не самої кількості інформації, а ступені її відмінності від фонової, як би контрастності. Так, наприклад, яскравість горіння сірника в день також як і вночі, але ймовірність виявити його різна.