Задача 1. Два точечных заряда 9 Q и -Q закреплены на расстоянии l = 50 см друг от друга. Третий заряд Q 1может перемещаться только вдоль прямой, проходящей через заряды. Определить положение заряда Q 1, при котором он будет находиться в равновесии. При каком знаке заряда Q 1равновесие будет устойчивым?
Решение. Заряд Q 1находится в равновесии в том случае, если геометрическая сумма сил, действующих на него, равна нулю. Это значит, что на заряд Q 1должны действовать две силы, равные по модулю и противоположные по направлению. Рассмотрим, на каком из трех участков I, II, III (Рис. 4) может быть выполнено это условие. Для определенности будем считать, что заряд Q 1— положительный.
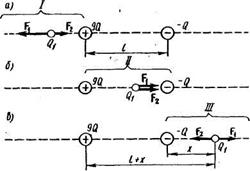
Рис. 5.
На участке I (рис. 5, а) на заряд Q 1будут действовать две противоположно направленные силы: 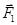 и
и 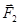 . Сила
. Сила 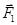 , действующая со стороны заряда 9 Q, в любой точке этого участка больше силы
, действующая со стороны заряда 9 Q, в любой точке этого участка больше силы 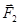 , действующей со стороны заряда
, действующей со стороны заряда
-Q, так как больший заряд 9Q находится всегда ближе к заряду Q 1, чем меньший (по модулю) заряд -Q. Поэтому равновесие на этом участке невозможно.
На участке II (рис. 4, б) обе силы 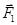 и
и 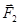 направлены в одну сторону — к заряду -Q. Следовательно, и на втором участке равновесие невозможно.
направлены в одну сторону — к заряду -Q. Следовательно, и на втором участке равновесие невозможно.
На участке III (рис. 4, в) силы 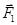 и
и 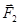 направлены в противоположные стороны, так же как и на участке I, но в отличие от него меньший заряд -Q всегда находится ближе к заряду Q 1,чем больший заряд 9 Q. Это значит, что можно найти такую точку на прямой, где силы
направлены в противоположные стороны, так же как и на участке I, но в отличие от него меньший заряд -Q всегда находится ближе к заряду Q 1,чем больший заряд 9 Q. Это значит, что можно найти такую точку на прямой, где силы 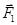 и
и 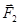 будут одинаковы по модулю, т. е.
будут одинаковы по модулю, т. е.
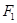 =
= 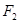 (1)
(1)
Пусть х и l+х — расстояние от меньшего и большего зарядов до заряда Q 1.Выражая в равенстве (1) 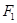 и
и 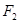 в соответствии с законом Кулона, получим
в соответствии с законом Кулона, получим
9 Q Q 1(l + x) 2 = Q Q 1 /x 2, или l + x = ± З х, откуда
x 1 = + l/ 2,
x 2 = - l/ 4.
Корень x 2не удовлетворяет физическому условию задачи (в этой точке силы 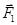 и
и 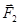 хотя и равны по модулю, но сонаправлены).
хотя и равны по модулю, но сонаправлены).
Определим знак заряда Q 1, при котором равновесие будет устойчивым. Равновесие называется устойчивым, если при смещении заряда от положения равновесия возникают силы, возвращающие его в положение равновесия. Рассмотрим смещение заряда Q 1 в двух случаях: когда заряд положителен и когда отрицателен.
Если заряд Q 1положителен, то при смещении его влево обе силы 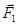 и
и 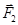 возрастают. Так как сила
возрастают. Так как сила 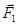 возрастает медленнее, то результирующая сила, действующая на заряд Q 1, будет направлена в ту же сторону, в которую смещен этот заряд, т. е. влево. Под действием этой силы заряд Q 1 будет удаляться от положения равновесия. То же происходит и при смещении заряда Q 1вправо. Сила
возрастает медленнее, то результирующая сила, действующая на заряд Q 1, будет направлена в ту же сторону, в которую смещен этот заряд, т. е. влево. Под действием этой силы заряд Q 1 будет удаляться от положения равновесия. То же происходит и при смещении заряда Q 1вправо. Сила 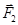 убывает быстрее, чем
убывает быстрее, чем 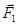 . Геометрическая сумма сил в этом случае направлена вправо. Заряд под действием этой силы также будет перемещаться вправо, т. е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.
. Геометрическая сумма сил в этом случае направлена вправо. Заряд под действием этой силы также будет перемещаться вправо, т. е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.
Если заряд Q 1отрицателен, то его смещение влево вызовет увеличение сил 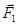 и
и 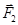 , но сила
, но сила 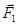 возрастает медленнее, чем
возрастает медленнее, чем 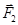 , т. е. |
, т. е. | 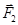 |>|
|>| 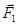 |. Результирующая сила будет направлена вправо. Под ее действием заряд Q 1 возвращается к положению равновесия. При смещении Q 1 вправо сила
|. Результирующая сила будет направлена вправо. Под ее действием заряд Q 1 возвращается к положению равновесия. При смещении Q 1 вправо сила 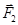 убывает быстрее, чем
убывает быстрее, чем 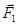 , т. е. |
, т. е. | 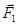 |>|
|>| 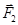 |. результирующая сила направлена влево и заряд Q 1 опять будет возвращаться к положению равновесия. При отрицательном заряде равновесие является устойчивым. Величина самого заряда Q 1несущественна.
|. результирующая сила направлена влево и заряд Q 1 опять будет возвращаться к положению равновесия. При отрицательном заряде равновесие является устойчивым. Величина самого заряда Q 1несущественна.
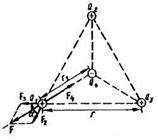
Рис. 6.
Задача 2. Три точечных заряда Q 1 = Q 2 = Q 3 = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q 4 нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?
Решение. Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы какой-нибудь один из трех зарядов, например Q 1,находился и равновесии. Заряд Q 1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулевому вектору (Рис. 6):
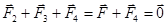 (1)
(1)
где 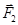 ,
, 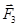 ,
, 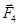 — силы, с которыми соответственно действуют на заряд Q 1 заряды Q 2, Q 3, Q 4;
— силы, с которыми соответственно действуют на заряд Q 1 заряды Q 2, Q 3, Q 4; 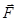 равнодействующая сил
равнодействующая сил 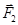 и
и 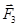
Так как силы 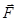 и
и 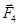 направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным: F - F 4 = 0, откуда F 4 = F. Выразив в последнем равенстве F через F 2, F 3 и учитывая, что F 3 = F 2, получим
направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным: F - F 4 = 0, откуда F 4 = F. Выразив в последнем равенстве F через F 2, F 3 и учитывая, что F 3 = F 2, получим
F 4 = F 2 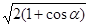 .
.
Применив закон Кулона и имея в виду, что Q 2 = Q 3 = Q 1, найдем
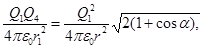
откуда Q 4= 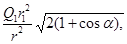 (2)
(2)
 Из геометрических построений в равностороннем треугольнике следует, что
Из геометрических построений в равностороннем треугольнике следует, что
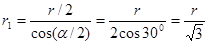 , cos α=cos 60°=l/2.
, cos α=cos 60°=l/2.
С учетом этого формула (2) примет вид
Q 4 = Q 1 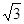 .
.
Произведем вычисления:
Q 4 = 10-9 / 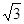 Кл = 5,77·10-10 Кл = 577 пКл.
Кл = 5,77·10-10 Кл = 577 пКл.
Задача 3. На тонком стержне длиной l = 20 см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится точечный заряд Q 1 = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность τ заряда на стержне.
Решение. Сила взаимодействия F заряженного стержня с точечным зарядом Q 1зависит от линейной плотности τ заряда на стержне. Зная эту зависимость, можно определить τ.
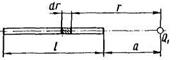
Рис. 7
При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (Рис. 7) малый участок dr с зарядом dQ = τdr. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона,
d F = 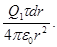
Интегрируя это выражение в пределах от a до a + l, получаем
F = 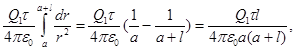
откуда 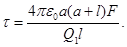
Проверим, дает ли расчетная формула единицу линейной плотности электрического заряда. Для этого в правую часть формулы вместо символов величин подставим их единицы:
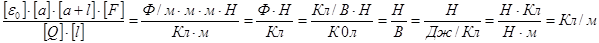
Найденная единица является единицей линейной плотности заряда.
Произведем вычисления:
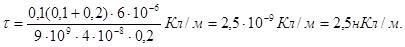
Задача 4. Два точечных электрических заряда Q 1 = 1 нКл и Q 2= - 2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга. Определить напряженность 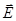 и потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от заряда Q 1на расстояние r 1= 9 см и от заряда Q 2 на r 2 = 7 см.
и потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от заряда Q 1на расстояние r 1= 9 см и от заряда Q 2 на r 2 = 7 см.
Решение. Согласно принципу суперпозиции электрических полей, поле, созданное зарядом, не зависит от присутствия других зарядов. Поэтому напряженность 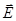 электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей
электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей 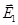 и
и 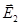 полей, создаваемых каждым зарядом в отдельности:
полей, создаваемых каждым зарядом в отдельности: 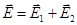 . Напряженности электрического поля, создаваемого в воздухе (ε = 1) зарядами Q 1 и Q 2, складываются.
. Напряженности электрического поля, создаваемого в воздухе (ε = 1) зарядами Q 1 и Q 2, складываются.
Вектор 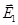 (Рис. 8.) направлен по силовой линии от заряда Q 1, так как этот заряд положителен; вектор
(Рис. 8.) направлен по силовой линии от заряда Q 1, так как этот заряд положителен; вектор 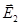 направлен также по силовой линии, но к заряду Q 2 так как этот заряд отрицателен.
направлен также по силовой линии, но к заряду Q 2 так как этот заряд отрицателен.
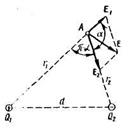
Рис. 8.
Модули векторов 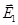 и
и 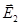 находим по формулам
находим по формулам
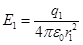 , (1)
, (1)
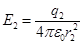 . (2)
. (2)
Модуль результирующего вектора 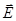 найдем по теореме косинусов:
найдем по теореме косинусов:
Е = 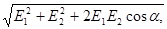 (3)
(3)
где α - угол между векторами 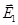 и
и 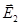 , который может быть найден из треугольника со сторонами r 1, r 2и d: cos α =
, который может быть найден из треугольника со сторонами r 1, r 2и d: cos α = 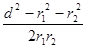 . В данном случае во избежание громоздких записей удобно значение cos α вычислить отдельно:
. В данном случае во избежание громоздких записей удобно значение cos α вычислить отдельно:
cos α = 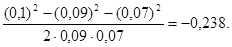
Подставляя выражение Е 1 из (1) и Е 2 из (2) в (3) и вынося общий множитель 1/(4 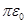 ) за знак корня, получаем
) за знак корня, получаем
Е = 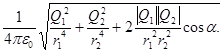 (4)
(4)
В соответствии с принципом суперпозиции электрических полей потенциал φ результирующего поля, создаваемого двумя зарядами Q 1 и Q 2, равен алгебраической сумме потенциалов;
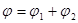 (5)
(5)
Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой
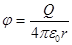 . (6)
. (6)
В нашем случае согласно формулам (5) и (6) получим
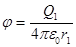 +
+ 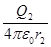 ,
,
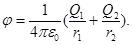
Произведем вычисления:
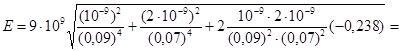
=3,58·103 В/м = 3,58 кВ/м;
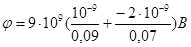 =-157 В.
=-157 В.
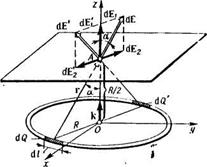
Рис. 9
Задача 5. По тонкому кольцу равномерно распределен заряд Q = 40 нКл с линейной плотностью τ = 50 нКл/м. Определить напряженность 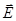 электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
Решение. Совместим координатную плоскость хoу с плоскостью кольца, а ось oz - с осью кольца (Рис. 9). На кольце выделим малый участок длиной dl. Так как заряд dQ = τ dl, находящийся на этом участке, можно считать точечным, то напряженность d 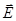 электрического поля, создаваемого этим зарядом, может быть записана в виде
электрического поля, создаваемого этим зарядом, может быть записана в виде
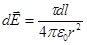 ,
,
где r — радиус-вектор, направленный от элемента dl к точке А.
Разложим вектор d 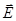 на две составляющие: d
на две составляющие: d 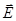 1, перпендикулярно плоскости кольца (сонаправленную с осью Oz), и d
1, перпендикулярно плоскости кольца (сонаправленную с осью Oz), и d 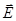 2, параллельную плоскости кольца (плоскости хoу), т. е.
2, параллельную плоскости кольца (плоскости хoу), т. е.
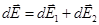
Напряженность Е электрического поля в точке А найдем интегрированием
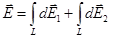 ,
,
где интегрирование ведется по всем элементам заряженного кольца. Заметим, что для каждой пары зарядов (dQ = dQ'), расположенных симметрично относительно центра кольца, векторы 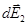 и
и 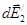 в точке А равны по модулю и противоположны по направлению:
в точке А равны по модулю и противоположны по направлению: 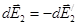 .Поэтому векторная сумма (интеграл)
.Поэтому векторная сумма (интеграл) 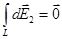 .
.
Составляющие 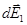 для всех элементов кольца сонаправлены с осью oz (единичным вектором
для всех элементов кольца сонаправлены с осью oz (единичным вектором 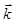 , определяющим направление оси Z), т.е.
, определяющим направление оси Z), т.е. 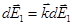 . Тогда
. Тогда
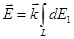 .
.
Так как dE = 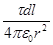 , r =
, r = 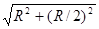 = =
= = 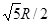 и cos α = (R/2)/ r = l/
и cos α = (R/2)/ r = l/ 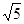 , то
, то
dE 1 = 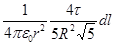 =
= 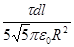 .
.
 2015-06-05
2015-06-05 3201
3201
