Для выполнения основных операций математического анализа в программе Mathematica предусмотрен набор команд, как с помощью клавиатуры, так и помощью палитр BasicInput и BasicCalculations. В таблицах 3-7 рассмотрены примеры реализации наиболее часто используемых действий, верхняя строка примеров представляет собой команду ввода, нижняя – вывода.
Таблица 3 – Нахождение пределов
| Действие | Реализация |
| Нахождение пределов | |
Нахождение предела 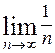
| 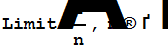
|
| Нахождение односторонних пределов | |
Нахождение предела 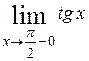 слева слева
| 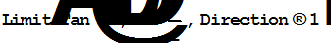 ¥
¥
|
Нахождение предела 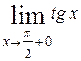 справа справа
| 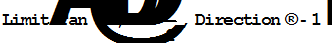 -¥
-¥
|
Таблица 4. Нахождение сумм рядов
| Набор с помощью клавиатуры | Набор с помощью палитры |
| Нахождение сумм рядов | |
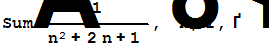
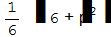
| 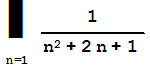
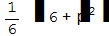
|
| Вычисление суммы в численном виде | |
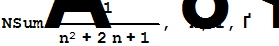 0.644934
0.644934
| 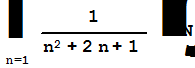 0.644934
0.644934
|
Замечание 1. Набор с помощью шаблонов палитр упрощает и ускоряет набор команд, а также уменьшает количество ошибок при наборе, так как шаблоны функций соответствуют общепринятым в математике обозначениям.
Замечание 2. Если программа Mathematica получит результат о расходимости ряда, то перед строкой вывода появится замечание: Sum does not converge, а строка вывода повторит запись исходного ряда.
Замечание 3. Если программа Mathematica не может вычислить аналитически, к чему именно сходится заданный ряд, но «считает», что он сходится, то строка вывода повторит запись исходного ряда. В этом случае можно рекомендовать получить результат численно.
Пример. С вычислением аналитически, к чему именно сходится ряд вида 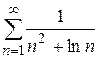 , программа Mathematica не «справилась», но «считает», что он сходится (замечание «Sum does not converge» не появилось). Строка вывода повторяет запись исходного ряда, численно был получен следующий результат:
, программа Mathematica не «справилась», но «считает», что он сходится (замечание «Sum does not converge» не появилось). Строка вывода повторяет запись исходного ряда, численно был получен следующий результат:
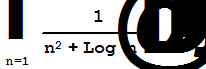
1.58462+0.ä
Таблица 5 – Дифференцирование
| Набор с помощью клавиатуры | Набор с помощью палитры |
| Нахождение производной | |
| D[Sin[x],x] Cos[x] | 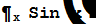 Cos[x]
Cos[x]
|
| Нахождение производной высших порядков | |
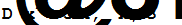 24 x
24 x
| 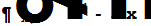 24 x
24 x
|
| Нахождение смешанной производной | |
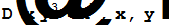
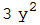
| 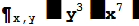
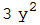
|
| Нахождение полного дифференциала | |
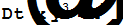
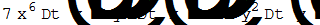
|
Замечание 4. Даже если задана функция от одной переменной, в команде нахождения производной необходимо указать переменную дифференцирования.
Таблица 6 – Интегрирование
| Набор с помощью клавиатуры | Набор с помощью палитры |
| Нахождение неопределенного интеграла | |
| Integrate[Sin[x],x] -Cos[x] | 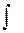 Sin[x]âx
-Cos[x] Sin[x]âx
-Cos[x]
|
| Вычисление определенного интеграла | |
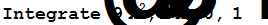
| 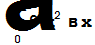
|
| Вычисление повторного интеграла | |
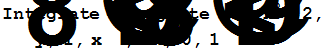 -4
-4
| 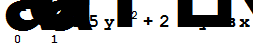 -4
-4
|
| Численное интегрирование | |
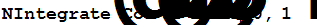 0.904524
0.904524
| 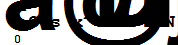 0.904524
0.904524
|
Замечание 5. Если программа Mathematica не может вычислить опреде-ленный интеграл аналитически, то строка вывода повторяет запись исходного интеграла. В этом случае можно рекомендовать получить результат численно.
Таблица 7 – Решение дифференциальных уравнений и систем уравнений
| Аналитическое решение дифференциальных уравнений |
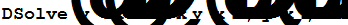
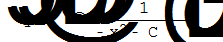
|
| Решение дифференциальных уравнений с начальными условиями |
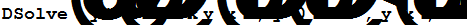
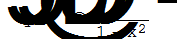
|
DSolve[{y''[x]+ 2y'[x]-3y[x]Š0,y[0]Š2,y'[0]Š1},y[x],x]
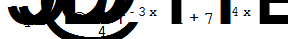
|
| Решение систем дифференциальных уравнений |
DSolve[{z'[x]Šz[x]-3y[x],y'[x]Š3z[x]+y[x]},{y[x],z[x]},x]
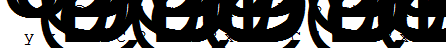
|
| Решение систем дифференциальных уравнений с начальными условиями |
DSolve[{z'[x]Šz[x]-3y[x],y'[x]Š3 z[x]+y[x],y[0]Š0,z[0]Š1}, {y[x],z[x]},x]
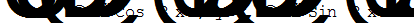
|
Замечание 6. При вводе функции DSolve следует обратить внимание на то, что и дифференциальные уравнения, и начальные условия записываются с двумя знаками равенства.
Замечание 7. При решении дифференциальных уравнений программа Mathematica часто выводит результат в очень громоздкой форме, которую можно значительно упростить, используя функцию Simplify. При этом сам результат можно не вносить в эту функцию как аргумент, а воспользоваться знаком %, т.е. Simplify[%]. Знак % означает ссылку на результат предыдущей по номеру строки.
Пример
DSolve[y''[x]+2y'[x]+10y[x]Š3Cos[x]+Sin[x],y[x],x]
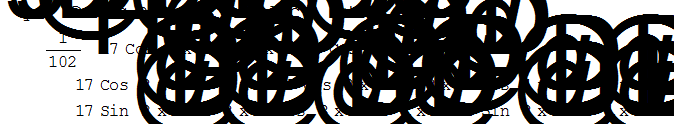
Simplify[%]
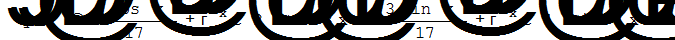
Замечание 8. Часто решение дифференциальных уравнений можно получить только в неявном виде, то есть решение, в котором функцию y невозможно выразить с помощью функции от x. Это может быть даже простое уравнение с разделяющимися переменными. Если при этом решение можно получить в явном виде относительно x, то имеет смысл в функции DSolve задать x как функции от y. Тогда программа Mathematica, возможно, «справится» с этим дифференциальным уравнением.
Пример
Относительно функции y программа Mathematica не может решить следующее дифференциальное уравнение:
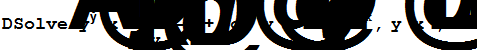

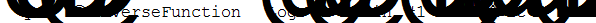
А относительно функции x программа Mathematica выдает следующий результат:
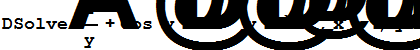
{{x[y]®Log[C[1]+Log[y]+Sin[y]]}}
Замечание 9. Следует помнить, что константы С[1], C[2] и т.д. в программе Mathematica могут быть выражены не таким же образом, как при решении пользователем.
 2015-06-05
2015-06-05 229
229








