Законы алгебры высказываний верные для любых высказываний А, В, С.
1. A  B = B
B = B  A – закон коммутативности пересечения.
A – закон коммутативности пересечения.
2. A  B = B
B = B  A – закон коммутативности объединения.
A – закон коммутативности объединения.
3. A  (B
(B  C) = (A
C) = (A  B)
B)  C – закон ассоциативности пересечения.
C – закон ассоциативности пересечения.
4. A  (B
(B  C) = (A
C) = (A  B)
B)  C – закон ассоциативности объединения.
C – закон ассоциативности объединения.
5. A  (B
(B  C) = (A
C) = (A  B)
B)  (A
(A  C)– закон дистрибутивности пересечения относительно объединения.
C)– закон дистрибутивности пересечения относительно объединения.
6. A  (B
(B  C) = (A
C) = (A  B)
B)  (A
(A  C) – закон дистрибутивности объединения относительно пересечения.
C) – закон дистрибутивности объединения относительно пересечения.
7. A  A = A – закон идемпотентности пересечения.
A = A – закон идемпотентности пересечения.
8. A  A = A – закон идемпотентности объединения.
A = A – закон идемпотентности объединения.
9. A  0 = 0. 10. A
0 = 0. 10. A  0 = A. 11. A
0 = A. 11. A  1= A. 12. A
1= A. 12. A  1 = 1.
1 = 1.
13. A 
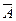 =0 – закон противоречия. 14. A
=0 – закон противоречия. 14. A 
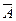 =1– закон исключенного третьего.
=1– закон исключенного третьего.
15. 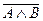 =
= 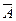

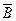 – закон де Моргана для дополнения пересечения.
– закон де Моргана для дополнения пересечения.
16. 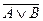 =
= 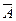

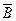 – закон де Моргана для дополнения объединения.
– закон де Моргана для дополнения объединения.
17. A  (B
(B  A) = A – закон поглощения. 18. A
A) = A – закон поглощения. 18. A  (B
(B  A) = A – закон поглощения.
A) = A – закон поглощения.
19. (A  B)
B)  (A
(A 
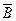 ) = A – закон склеивания. 20. (A
) = A – закон склеивания. 20. (A  B)
B)  (A
(A 
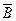 ) = A – закон склеивания.
) = A – закон склеивания.
21. A = 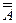 – закон инволюции. 22.
– закон инволюции. 22. 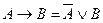 23.
23. 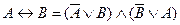
Замечание 1. Законы де Моргана можно распространить на большее число
множеств.
Замечание 2. Используя законы коммутативности и ассоциативности можно несколько конъюнкций выполнять в любом порядке 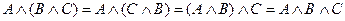 . Замечание 3. Используя законы коммутативности и ассоциативности можно несколько дизъюнкций выполнять в любом порядке
. Замечание 3. Используя законы коммутативности и ассоциативности можно несколько дизъюнкций выполнять в любом порядке 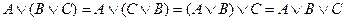 .
.
|
|
|
 2015-06-05
2015-06-05 316
316








