2015-06-05
525
Дизъюнктивные и конъюнктивные нормальные формы алгебры высказываний (ДНФ и КНФ). Конъюнктивным одночленом от переменных х 1, х 2, …, хп называется конъюнкция этих переменных или их отрицаний.
Дизъюнктивным одночленом от переменных х 1, х 2, …, хп называется дизъюнкция этих переменных или их отрицаний.
Формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных конъюнктивных одночленов, называется дизъюнктивной нормальной формой (ДНФ) данной формулы.
Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных дизъюнктивных одночленов, называется конъюнктивной нормальной формой (КНФ) данной формулы.
Для каждой формулы алгебры высказываний можно найти множество дизъюнктивных и конъюнктивных нормальных форм
Алгоритм построения ДНФ и КНФ.
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
1. 
;
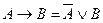2. 
.
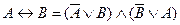
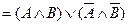2) Заменить сложные отрицания на простые с помощью законов
3. 
= 
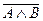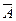
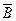;4.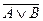 
= 
;
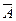
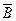3) Избавиться от знаков двойного отрицания.
4)Применить, если нужно, к операциям конъюнкция и дизъюнкции свойства дистрибутивности и формулы поглощения.
