Задача 3.1 Построить сокращенную ДНФ для функции, таблица истинности которой имеет следующий вид:
| x | y | z |  f(x,y,z) f(x,y,z)
|
Решение.
Построение СДНФ. Функция принимает значение 1 на кортежах (001), (010), (101). Кортежу (001) соответствует элементарная конъюнкция  . Кортежу (010) соответствует элементарная конъюнкция
. Кортежу (010) соответствует элементарная конъюнкция 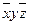 . Кортежу (101) соответствует элементарная конъюнкция
. Кортежу (101) соответствует элементарная конъюнкция 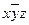 . Получаем СДНФ f(x,y,z)=
. Получаем СДНФ f(x,y,z)=  ˅
˅ 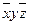 ˅
˅ 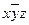 .
.
Построение СКНФ. Функция принимает значение 0 на кортежах (000), (011), (110), (111). Кортежу (000) соответствует элементарная дизъюнкция x˅y˅z. Кортежу (011) - x˅ 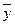 ˅
˅ 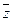 , кортежу (100) -
, кортежу (100) - 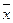 ˅y˅z, кортежу (110) -
˅y˅z, кортежу (110) - 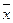 ˅
˅ 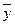 ˅z, кортежу (111) -
˅z, кортежу (111) - 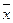 ˅
˅ 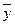 ˅
˅ 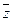 .
.
Получаем СКНФ  f(x,y,z) =(x˅y˅z)(x˅
f(x,y,z) =(x˅y˅z)(x˅ 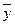 ˅
˅ 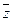 )(
)(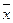 ˅y˅z)(
˅y˅z)(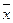 ˅
˅ 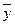 ˅z)(
˅z)(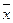 ˅
˅ 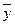 ˅
˅ 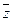 ). Далее проводим упрощение по алгоритму. Перемножение лучше начинать со скобок, которые отличаются всего одной переменной (например, z и
). Далее проводим упрощение по алгоритму. Перемножение лучше начинать со скобок, которые отличаются всего одной переменной (например, z и 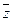 ). Поэтому поменяем местами 2-ую и 3-ю скобки. Получаем сокращенную ДНФ
). Поэтому поменяем местами 2-ую и 3-ю скобки. Получаем сокращенную ДНФ 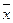 y
y 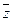 ˅
˅ 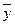 z.
z.
 2015-06-05
2015-06-05 394
394








