Ротор векторного поля

Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем.

Обозначается

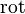(в русскоязычной литературе) или

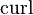(в англоязычной литературе),

а также — как векторное умножение дифференциального оператора набла на векторное поле:

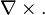
Результат действия этого оператора на конкретное векторное поле F называется ротором поля F или просто ротором F и представляет собой новое векторное поле:

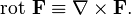
Поле rot F (длина и направление вектора rot F в каждой точке пространства) характеризует в некотором смысле^[3] вращательную составляющую поля F соответственно в каждой точке.

Ротор (вихрь) векторного поля

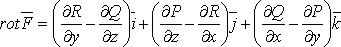
или в символическом виде

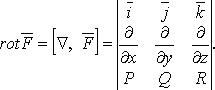
Свойства ротора

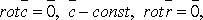
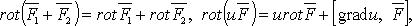
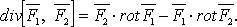
29) Дифференцированное уравнение с разделяющимися переменными.

30) Неоднородное линейное уравнение 1 порядка. Решение методом Бернулли.

31) Неоднородное линейное уравнение 1 порядка. Решение методом Лагранжа.

32) Уравнение Бернулли и его решение.
Обыкновенное дифференциальное уравнение вида:

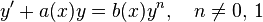
называется уравнением Бернулли (пр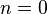и или 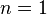получаем неоднородное или однородное линейное уравнение).

При 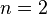является частным случаем уравнения Риккати. Названо в честь Якоба Бернулли, опубликовавшего это уравнение в 1695 году.

Метод решения с помощью замены, сводящей это уравнение к линейному, нашёл его брат Иоганн Бернулли в 1697 году.

Первый способ: Разделим все члены уравнения на

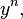
получим

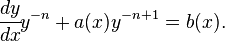
Делая замену

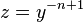
и дифференцируя, получаем:

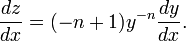
Это уравнение приводится к линейному:

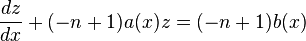
и может быть решено методом Лагранжа (вариации постоянной) или методом интегрирующего множителя.

Второй способ: Заменим

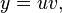
тогда:

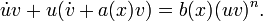
Подберем 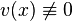так, чтобы было

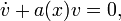
для этого достаточно решить уравнение с разделяющимися переменными 1-го порядка. После этого для определен 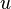получаем уравнение 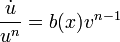— уравнение с разделяющимися переменными.

33) Уравнение в полных дифференциалах и его решение.

34) Уравнение с интегрирующим множителем.
Рассмотрим дифференциальное уравнение вида

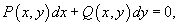
где P (x,y) и Q (x,y) − функции двух переменных x и y, непрерывные в некоторой области D. Если

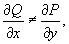
то уравнение не будет являться уравнением в полных дифференциалах. Однако мы можем попробовать подобрать так называемый интегрирующий множитель, представляющий собой функцию µ (x,y), такую, что после умножения на нее дифференциальное уравнение преобразуется в уравнение в полных дифференциалах. В таком случае справедливо равенство:

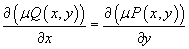
Это условие можно записать в виде:

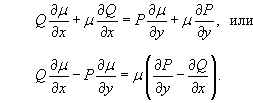
Последнее выражение представляет собой уравнение в частных производных первого порядка, которое определяет интегрирующий множитель µ (x,y).

К сожалению, не существует общего метода нахождения интегрирующего множителя. Однако можно упомянуть некоторые частные случаи, для которых можно решить полученное уравнение в частных производных и, в результате, определить интегрирующий множитель.

1. Интегрирующий множитель зависит от переменной x: µ = µ (x).

В этом случае мы имеем 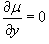, поэтому уравнение для µ (x,y) можно записать в виде:

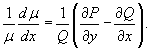
Правая часть этого уравнения должна быть только функцией от x. Функцию µ (x) можно найти, интегрируя последнее уравнение.

2. Интегрирующий множитель зависит от переменной y: µ = µ (y).

Аналогично, если 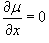, то мы получаем обыкновенное дифференциальное уравнение, определяющее интегрирующий множитель µ:

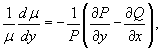
где правая часть зависит только от y. Функция µ (y) находится интегрированием данного уравнения.

3. Интегрирующий множитель зависит от определенной комбинации переменных x и y: µ = µ (z(x,y)).

Новая функция z (x,y) может быть, например, типа:

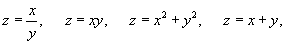
и так далее.

Здесь важно, что интегрирующий множитель µ (x,y) будет являться некоторой функцией одной переменной z:

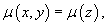
и может быть найден из дифференциального уравнения:

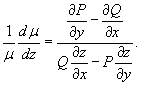
Предполагается, что правая часть уравнения зависит только от z и знаменатель не равен нулю.

Ниже мы рассмотрим некоторые частные случаи уравнения

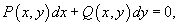
для которых можно найти интегрирующий множитель. Общие условия существования интегрирующего множителя выводятся в теории групп Ли.
35) Уравнение 2 порядка, допускающее понижение порядка и его решение.

36) Теорема о структуре общего решения линейного однородного дифференцированного уравнения вида { }

37) Теорема о структуре общего решения линейного неоднородного дифференцированного уравнения 2 порядка.