Функция нескольких производных. Вычисление частных производных

Пусть задана функция z = ƒ (х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δх, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆_хz. Итак,

Δ_хz=ƒ(х+Δх;у)-ƒ(х;у).

Аналогично получаем частное приращение z по у:

Δ_уz=ƒ(x;у+Δу)-ƒ(х;у).

Полное приращение Δz функции z определяется равенством

Δz = ƒ(х + Δх;у + Δу)- ƒ(х; у).

Если существует предел

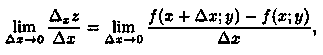
то он называется частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов:

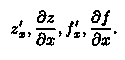
Частные производные по х в точке М₀(х₀;у₀) обычно обозначают символами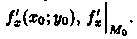

Аналогично определяется и обозначается частная производная от z=ƒ(х;у) по переменной у:

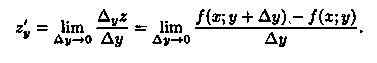
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции ƒ(х;у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).

15) Дифференцирование неявно заданной функции.

16) Экстремум функции двух переменных.

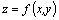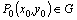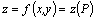Пусть функция определена в некоторой области G и точка . Функция имеет в точке 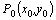максимум, если существует такая окрестность этой точки, что для всех точек 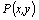этой окрестности, отличных от 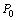, выполняется неравенство 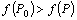. Аналогично определяется минимум функции. Максимум и минимум функции называются экстремумами функции. Теорема (необходимое условие экстремума). Если 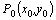– точка экстремума функции 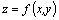, то частные производные 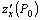и 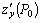в этой точке равны нулю или не существуют. 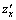Точки, в которых частные производные и 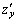обращаются в нуль или не существуют, называются критическими точками этой функции. Сформулированный признак не является достаточным: не обязательно критическая точка является точкой экстремума. Чтобы проверить, есть ли экстремум в критической точке, используют следующую теорему (достаточное условие экстремума). Пусть в некоторой области, содержащей точку 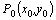, функция 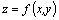имеет непрерывные частные производные до 3–го порядка включительно и 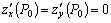. Обозначим: 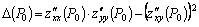. Тогда 1) если 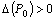, то функция имеет экстремум в точке 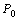, причем это максимум, если 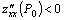и минимум, ес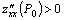ли ; 2) если 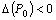, то экстремума в точке 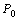нет; 3) если 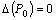, требуется дополнительное исследование (экстремум в точке 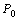может быть или не быть).