2015-06-26
1428
Выберем инерциальную систему отсчета, связанную с Землёй. Укажем все силы, действующие на грузы и блок. Т.к. нам предстоит рассмотреть поступательное движение грузов и вращательное движение блока, одну координатную ось направим вертикально вниз (ОХ), а другую (OZ) – перпендикулярно плоскости рисунка от нас вдоль оси блока*). Тогда в проекциях на эти оси соответствующие уравнения движения будут иметь вид:
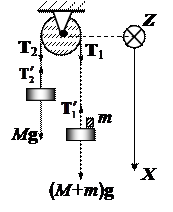
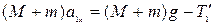(1)
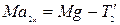(2)
(2й закон Ньютона),
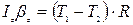(3)
(уравнение динамики вращательного движения барабана). Здесь Iz – момент инерции блока относительно оси Z.
Знак проекций моментов сил Т 1 и Т 2 выбран с учетом направления оси Z: проекция вектора момента силы Т 1 относительно любой точки на этой оси положительна, а силы Т 2 – отрицательна.
Cила натяжения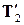 
, с которой нить действует на груз, равна по модулю силе Т 2, с которой нить действует на блок. Также обстоит дело и с силами 
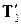и Т 1. Это следует из условия невесомости нити. Уравнения кинематической связи можно получить, выразив длину нити через координаты тел системы:
L = x 1 + pR + x 2.
Дифференцируя это равенство дважды по времени и учитывая нерастяжимость нити (L = const), получаем связь между проекциями линейных ускорений грузов:
а 1 х = - а 2 х = а. (4)
Для того, чтобы вышеприведенная система уравнений была полной, необходимо связать линейное ускорение поступательно движущихся грузов с угловым ускорением вращающегося блока. Т.к. в соответствии с выбором направления оси Z момент силы Т 1 обеспечивает блоку положительную проекцию углового ускорения bz, то проекция ускорения первого груза также положительна а 1 х > 0. Вспомним из кинематики, как связано тангенциальное ускорение точки при движении по окружности с её угловым ускорением:
аt =b × R.
Нить не скользит по поверхности блока, поэтому её точки имеют то же самое ускорение. Линейное ускорение точек нити на её вертикальных участках имеет такое же значение. А в силу нерастяжимости нити мы можем и для ускорений грузов окончательно записать уравнение кинематической связи:
а =b × R. (5)
Совместное решение уравнений (1) - (5) приводит к искомому результату для момента инерции блока:
.
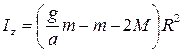Задача
3.3. Найти ускорение центра масс шара массой m, скатывающегося по наклонной плоскости, образующей угол a с горизонтом. Коэффициент трения между поверхностью шара и наклонной плоскостью равен m.
Решение
Выберем инерциальную систему отсчета, связанную с Землей. Одну из осей (X)неподвижной декартовой системы координат направим вдоль направления качения шара, т.е. парал-лельно плоскости, две другие – перпендикулярно к ней (см. рис.).
Силы, действующие на шар, изображены на рисунке. Уравнения динамики поступательного движения имеют вид:
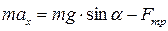, (1)
may = F p– mg ×cos a, ay = 0, (2)
где aх и ay – соответствующие проекции ускорения центра масс шара. Относительно оси, проходящей через центр масс перпен-дикулярно плоскости качения, момент имеет только сила трения:
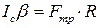. (3)
Для дальнейшего необходимо уточнить характер движения шара. Если проскальзывание отсутствует, то Fтр является силой трения покоя и 0 £ Fтр £ mF р, где m – коэффициент трения скольжения. Следовательно Fтр представляет собой, наряду с aх, F ри b неизвестную величину. Для полноты системы необходимо добавить ещё одно уравнение. Отсутствие проскальзывания позволяет связать линейное и угловое ускорения шара: ах = b × R.
Решая полученную систему, получаем:
.
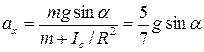При наличие проскальзывания величины ах и b больше не связаны. Дополнительным уравнением является выражение для силы трения скольжения:
,
.
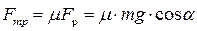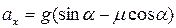
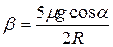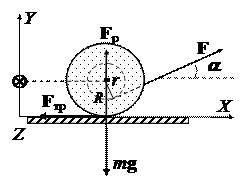
3.4. (Задача о «послушной катушке») На горизонтальной поверхности лежит катушка с намотанной на нее нитью. Катушка движется по поверхности без проскальзывания. Найти ускорение центра масс катушки. Массу катушки m, ее момент инерции I относительно собственной оси и угол α считать заданными. При каком угле α катушка останется неподвижной?
Решение
Укажем все силы, действующие на катушку. Выберем инерциальную систему отсчета, связанную с Землёй. Т.к. катушка может совершать плоское движение, представим его как совокупность поступательного и вращательного. Направим одну из координатных осей этой системы отсчёта вдоль горизонтальной поверхности (OX), вторую – вертикально вверх (OY). Так как моменты всех сил приложенных к телу и его возможное угловое ускорение направлены вдоль оси катушки, направим третью координатную ось OZ перпендикулярно плоскости рисунка от нас через центр катушки.
Запишем уравнения движения катушки в проекциях на выбранные оси координат (ах – ускорение центра масс катушки):
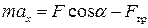, (1)
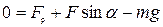(2)
(2й закон Ньютона, поступательное движение);
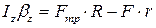(3)
(уравнение динамики вращательного движения катушки). Здесь Iz – момент инерции блока относительно оси Z. Обратим внимание на знаки проекций моментов сил и углового ускорения на ось Z, а также на согласованность знаков проекций линейного и углового ускорений катушки – положительный знак проекции линейного ускорения соответствует ускоренному вращению катушки по часовой стрелке, т.е. положительной проекции линейного ускорения оси катушки аx.
Условие отсутствия проскальзывания катушки позволяет связать проекции этих ускорений:
аx =bz × R. (5)
Совместное решение уравнений (1) - (5) позволяет определить искомое ускорение центра катушки
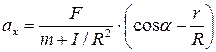. (6)
Проанализируем полученный результат. Видно, что знак проекции определяется соотношением величин cos a и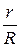 
. При малых углах наклона “тянущей” нити, когда cos a > 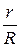, катушка катится с ускорением вправо. Если же cos a < 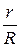(наклон нити большой), ускорение направлено влево. Наконец, при 
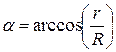ускорение катушки равно нулю и при соответствующих начальных условиях она может оставаться неподвижной.
