Диффузионный рост наночастиц

Рассмотрим сферическую наночастицу радиуса R, находящуюся в жидкости. Пусть в жидкости растворено вещество с плотностью 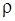. На поверхности частицы плотность растворенного вещества равна 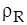, вдали от частицы плотность этого вещества равна 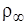. Считая, что плотность растворенного вещества в окрестности частицы зависит от радиальной координаты 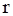, которая отсчитывается от центра частицы, запишем уравнение стационарной диффузии

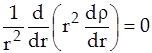. (1)

Решая это уравнение с граничными условиями

,

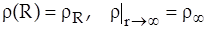получаем распределение концентрации растворенного вещества в окрестности частицы в виде

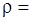(2)

График этой зависимости имеет вид

Рис.1. Зависимость плотности вещества, растворенного в жидкости, от расстояния до центра частицы

Для расчета диффузионного роста частицы найдем плотность массового потока к ее поверхности

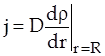= (3)

где 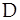- коэффициент диффузии растворенного вещества.

Плотность массового потока представляет собой массу, проходящую через единицу площади за единицу времени. Тогда через всю поверхность частицы за единицу времени проходит масса

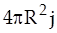= (4)

Приравнивая это выражение к скорости изменения массы частицы

,

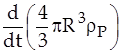где 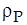- плотность вещества частицы, 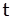- время, получаем дифференциальное уравнение, описывающее диффузионный рост частицы

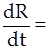(5)

Интегрируя это уравнение с учетом начального условия

,

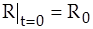получаем зависимость радиуса частицы от времени в виде

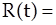(6)

График этой зависимости имеет вид

Рис.2. Зависимость радиуса частицы от времени в ходе ее диффузионного роста

Используя (6), определим время 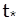, за которое квадрат радиуса частицы 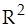возрастет вдвое

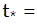(7)

Для того чтобы мы могли использовать стационарное уравнение диффузии (1) вместо нестационарного уравнения диффузии

,

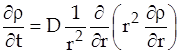время установления стационарного режима диффузии 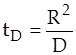должно быть мало, по сравнению со временем 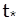(характерное время изменения радиуса частицы). Условие 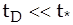представим в виде

(8)