Задание 5. Укажите наименьшее основание системы счисления, в которой запись числа 30 трехзначна

Укажите наименьшее основание системы счисления, в которой запись числа 30 трехзначна.

Решение:

1) обозначим через 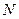неизвестное основание системы счисления, тогда запись числа 30 в этой системе имеет вид

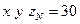
2) вспомним алгоритм перевода числа из системы счисления с основанием 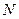в десятичную систему: расставляем сверху номера разрядов и умножаем каждую цифру на основание в степени, равной разряду:

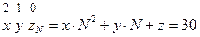
3) поскольку запись трехзначная, 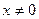, поэтому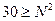

4) с другой стороны, четвертой цифры нет, то есть, в третьем разряде – ноль, поэтому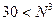

5) объединяя последние два условия, получаем, что искомое основание 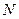удовлетворяет двойному неравенству

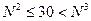
6) учитывая, что 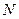– целое число, методом подбора находим целые решения этого неравенства; их два – 4 и 5:

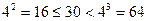
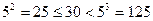
7) минимальное из этих значений – 4

8) таким образом, верный ответ – 4.

Решение (без подбора):

1) выполним п.1-4 так же, как и в предыдущем варианте решения

2) найдем первое целое число, куб которого больше 30; это 4, так как

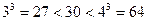
3) проверяем второе неравенство: 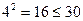, поэтому в системе счисления с основанием 4 запись числа 30 трехзначна

4) таким образом, верный ответ – 4.