Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Общий подход:
· вспомним алгоритм перевода числа из десятичной системы в систему с основанием 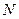 (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на
(см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на 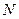 , а две младших цифры – это остаток от деления на
, а две младших цифры – это остаток от деления на 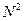 и т.д.
и т.д.
· в данном случае 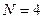 , остаток от деления числа на
, остаток от деления числа на 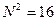 должен быть равен 114 = 5
должен быть равен 114 = 5
· потому задача сводится к тому, чтобы определить все числа, которые меньше или равны 25 и дают остаток 5 при делении на 16
Решение (вариант 1, через десятичную систему):
1) общий вид чисел, которые дают остаток 5 при делении на 16:
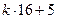
где 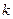 – целое неотрицательное число (0, 1, 2, …)
– целое неотрицательное число (0, 1, 2, …)
2) среди всех таких чисел нужно выбрать те, что меньше или равны 25 («не превосходят 25»); их всего два: 5 (при 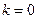 ) и 21 (при
) и 21 (при 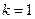 )
)
3) таким образом, верный ответ – 5, 21.
Возможные проблемы: · выражение «не превосходящие 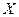 » означает «меньшие или равные » означает «меньшие или равные 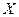 », а не строго меньшие », а не строго меньшие 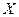 · остаток, состоящий из нескольких цифр (здесь – 114), нужно не забыть перевести в десятичную систему · найденные числа нужно записать именно в порядке возрастания, как требуется · остаток, состоящий из нескольких цифр (здесь – 114), нужно не забыть перевести в десятичную систему · найденные числа нужно записать именно в порядке возрастания, как требуется |
Решение (вариант 2, через четверичную систему):
1) переведем 25 в четверичную систему счисления: 25 = 1214, все интересующие нас числа не больше этого значения
2) из этих чисел выделим только те, которые заканчиваются на 11, таких чисел всего два:
это 114 = 5 и 1114 = 21
3) таким образом, верный ответ – 5, 21.
| Возможные проблемы: · есть риск случайно «забыть» какое-то число или найти «лишнее» (в данном случае – большее 25) · можно сделать ошибки при переводе чисел из четверичной системы в десятичную или вообще «забыть» перевести |
 2015-06-26
2015-06-26 4773
4773
