2015-06-26
1931
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Общий подход:
· здесь обратная задача – неизвестно основание системы счисления, мы обозначим его через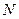 
· поскольку последняя цифра числа – 2, основание должно быть больше 2, то есть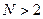 
· вспомним алгоритм перевода числа из десятичной системы в систему с основанием 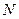(см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на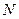
Решение:
1) итак, нужно найти все целые числа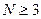 
, такие что остаток от деления 23 на 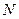равен 2, или (что то же самое)
(*)
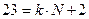где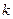 
– целое неотрицательное число (0, 1, 2, …);
2) сложность в том, что 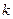и , и 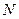неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
3) из формулы (*) получаем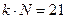 
, так что задача сводится к тому, чтобы найти все делители числа 21, которые больше 2
4) в этой задаче есть только три таких делителя: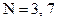 
и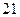 
5) таким образом, верный ответ – 3, 7, 21.
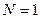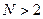Возможные проблемы: · нужно учесть, что основание системы счисления должно быть больше любой цифры числа, поэтому делитель  не подходит (должно быть ) · числа нужно записывать в ответе в порядке возрастания, как требуется по условию |
