Неустойчивость границы твердого тела при его диффузионном росте

Зададим границу твердого тела в виде 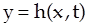, - см. рис.1.

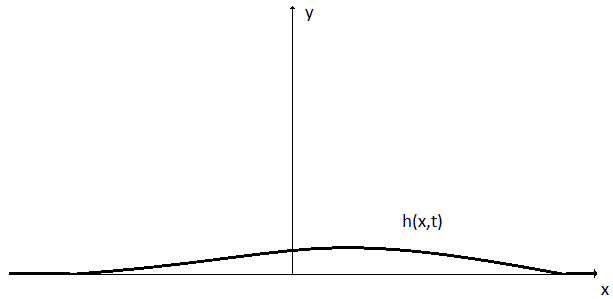
Рис.1 Граница твердого тела

Область 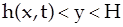заполнена жидкостью, в которой растворено вещество с плотностью 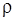. Будем считать, что на поверхности твердого тела плотность растворенного вещества равна нулю, а на расстоянии 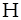от поверхности плотность вещества равна :

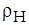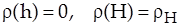. (1)

Уравнение диффузии в жидкости запишем в виде

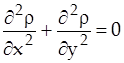. (2)

Для расчета концентрации растворенного вещества в жидкости будем решать уравнение (2) с граничными условиями (1). При этом воспользуемся малостью возмущения формы границы .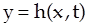

В нулевом приближении граница плоская (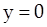), концентрация 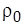зависит только от вертикальной координаты 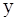, уравнение (2) и граничные условия (1) приобретают вид

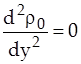, (3)

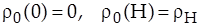. (4)

Интегрируя (3) с граничными условиями (4), получаем

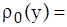(5)

Решение уравнения (2) с граничными условиями (1) будем искать в виде

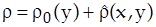, (6)

где 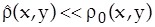. Подставляя (6) в (1), (2), получаем

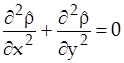. (7)

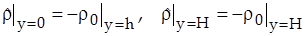. (8)

Применим к (7), (8), преобразование Фурье по координате :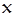

.

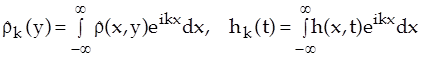Тогда получаем

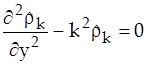. (9)

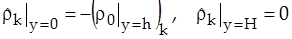, (10)

где под 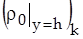подразумевается следующее. Нужно взять выражение (5) для 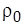, подставить в него 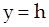, а от полученного выражения взять образ по Фурье.

Решение уравнения (9) с граничными условиями (10) имеет вид

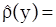(11)