Прямая в пространстве

В зависимости от способа задания прямой в пространстве можно рассматривать различные ее уравнения:

1. Векторно-параметрическое уравнение прямой. Пусть прямая проходит через точку M₀(x₀,y₀,z₀) параллельно вектору s(m,n,p), а M(x,y,z) любая точка этой прямой.

Если r₀ и r – радиусы-векторы точек M₀ и M, то справедливо векторное равенство:

r=r₀+t•s (-∞ < t < +∞) (7)

которое получается по правилу сложения векторов. Уравнение (7) называется векторно-параметрическим уравнением прямой, s – направляющим вектором прямой (7), t – параметром.

2. Параметрические уравнения прямой. Из уравнения (7) получаем три скалярных уравнения:

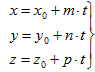(8)

которые называются параметрическими уравнениями прямой.

3. Канонические уравнения прямой. Разрешая уравнения в системе (8) относительно t и приравнивая полученные отношения, приходим к конечным уравнениям прямой:

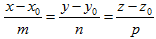(9)

4. Уравнения прямой в пространстве, проходящей через две точки.

Если прямая проходит через точки M₁(x₁,y₁,z₁) и M₂(x₂,y₂,z₂), то её уравнения можно записать в виде

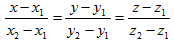(10)

5. Общие уравнения прямой в пространстве. Две пересекающиеся плоскости

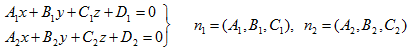(11)

где n₁ и n₂ не параллельны, определяют прямую. Уравнение (11) называются общими уравнениями прямой в пространстве.

Направляющий вектор s прямой, заданной уравнениями (11), определяется по формуле

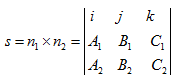
а координаты какой-либо точки M₀(x₀,y₀,z₀), лежащей на этой прямой, можно найти как решение системы (11). Тогда уравнения данной прямой можно записать в канонической форме.

Если прямые заданы каноническими уравнениями:

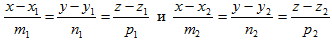
то величина угла φ между ними определяется из формулы:

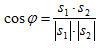(12)

Теперь можно записать условие перпендикулярности прямых s₁•s₂=0, a условие параллельности s₁||s₂, а условия их совпадения s₁||s₂||M₁M₂, где М₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂), а s₁,s₂ – направляющие векторы.

Необходимое и достаточное условие пересечения не параллельных прямых заданных в каноническом виде

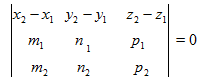(13)

Если условие (26) не выполняется, то прямые скрещивающиеся.

Расстояние h от точки М₁(x₁,y₁,z₁) до прямой, проходящей через точку M₀(x₀,y₀,z₀) в направлении вектора s(m,n,p) вычисляется по формуле:

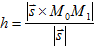(14)

Углом между прямой и плоскостью называется угол между прямой и ортогональной проекцией на плоскость.

Величина угла 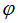между прямой и плоскостью вычисляется по формуле:

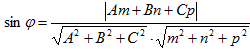(15)

Пример 15. Составить уравнение плоскости, проходящей через точку Р(1,0,2) перпендикулярно к двум плоскостям 2x–y+3z–1=0 и 3x+6y+3z-5=0

Так как коэффициенты плоскостей не пропорциональны, то они пересекаются, тогда направляющий вектор линий пересечения находим из векторного произведения нормалей двух плоскостей т.е.

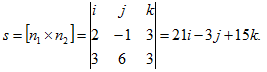
Тогда этот вектор будет нормалью искомой плоскости и согласно этому находим 7x–y-5z=0.

Пример 16. Записать уравнение плоскости, проходящей через прямую 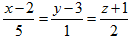перпендикулярно к плоскости x+4y-3z+7=0.

Искомая плоскость проходит через точку М₀(2,3,-1) на прямой и через направляющий вектор прямой s=(5,1,2) и через нормаль данной плоскости n=(1,4,-3). Тогда из условия компланарности трех векторов М₀М, s и n находим:

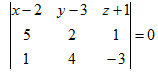, откуда 11x-17y-19z+10=0.

Вопросы для самоконтроля.

1. Какой вид имеет условие параллельности и перпендикулярности двух плоскостей?
2. По какой формуле находят угол между прямой и плоскостью?
3. Как выглядит каноническое уравнение прямой?
4. Запишите формулы: угла между плоскостями, уравнения плоскости, параметрического уравнения прямой.

Использованная литература.

Конспект лекций по высшей математике: полный курс. Письменный Д.Т. 4-е изд. — М.: Айрис-пресс, 2006. — 608 с.