Пусть плоскость 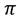 и прямая
и прямая 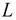 заданы уравнениями:
заданы уравнениями:
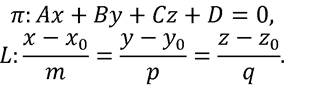
Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и её проекцией на плоскость.
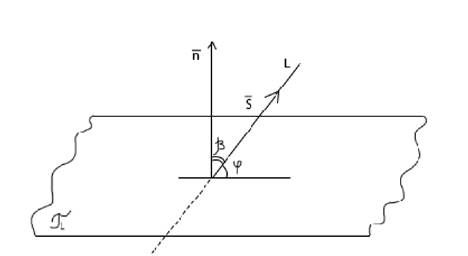
Обозначим через 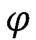 угол между прямой
угол между прямой 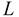 и плоскостью
и плоскостью 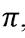 а
а 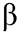 - угол между векторами
- угол между векторами 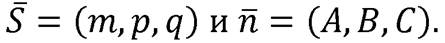
Тогда 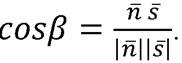 Найдём
Найдём 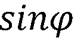
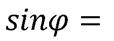 =
= 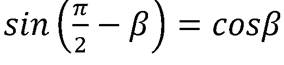 . Отсюда с учётом, что
. Отсюда с учётом, что 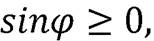 получаем:
получаем:
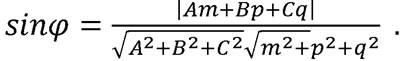 ) Условия параллельности и перпендикулярности прямой и плоскости:
) Условия параллельности и перпендикулярности прямой и плоскости:
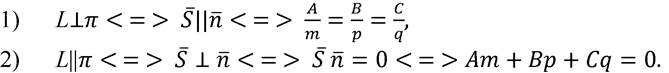
Пример1. Найти взаимное расположение прямой  и плоскости
и плоскости 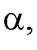 если: а)
если: а) 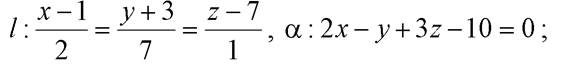
б) 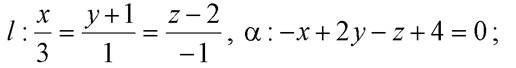
в) 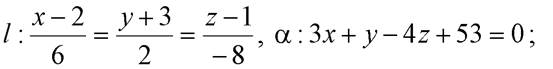
г) 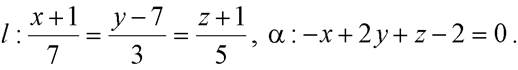
Решение:
а)Проверим, являются ли прямая 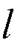 и плоскость
и плоскость 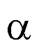 параллельными, вычислим для этого скалярное произведение направляющего вектора
параллельными, вычислим для этого скалярное произведение направляющего вектора 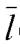 ={2; 7; 1} и нормали
={2; 7; 1} и нормали 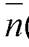 ={2; - 1; 3}:
={2; - 1; 3}: 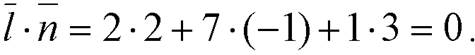 Видим, что
Видим, что 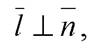 следовательно,
следовательно, 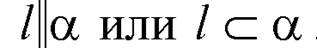 . Проверим, лежит ли прямая l в плоскости α, подставив
. Проверим, лежит ли прямая l в плоскости α, подставив
координаты точки M 0(1; –3; 7) в уравнение плоскости: 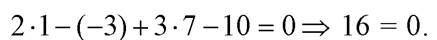 Мы получили неверное равенство, следовательно,
Мы получили неверное равенство, следовательно, 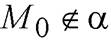 и
и 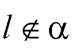 . Таким образом,
. Таким образом, 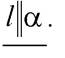
б)В этом случае 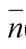 ={-1; 2; -1},
={-1; 2; -1}, 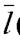 ={3; 1; -1}, M 0(0; –1; 2). Проверим, перпендикулярны ли векторы
={3; 1; -1}, M 0(0; –1; 2). Проверим, перпендикулярны ли векторы 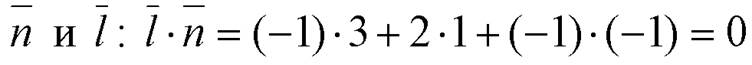 .Таккак
.Таккак 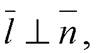 следовательно,
следовательно, 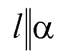 или
или 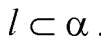 Подставим координаты точки
Подставим координаты точки 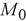 в уравнение плоскости
в уравнение плоскости 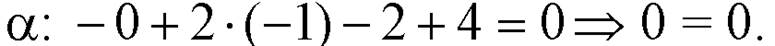 Полученное верное равенство говорит о том, что
Полученное верное равенство говорит о том, что 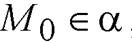 , следовательно,
, следовательно, 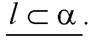
в) В этом случае 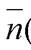 ={3; 1; - 4},
={3; 1; - 4}, 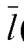 ={6; 2; -8},
={6; 2; -8},
M 0(2;–3;1).Проверим,чемуравно скалярное произведение векторов 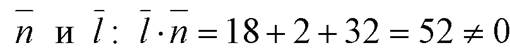 , то
, то
есть векторы 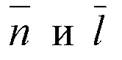 не перпендикулярны. Следовательно, прямая l не может
не перпендикулярны. Следовательно, прямая l не может
ни лежать в плоскости α, ни быть ей параллельной. Проверяя, коллинеарны ли векторы 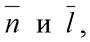 видим, что
видим, что 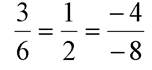 (их координаты пропорциональны), то есть
(их координаты пропорциональны), то есть 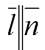 . Значит,
. Значит, 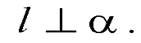
Можно найти точку пересечения прямой  и плоскости
и плоскости  решив совместно их уравнения:
решив совместно их уравнения: 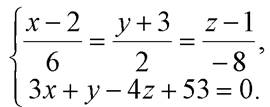 Для упрощения решения введем параметр в уравнении прямой (перейдем к параметрическому уравнению):
Для упрощения решения введем параметр в уравнении прямой (перейдем к параметрическому уравнению):
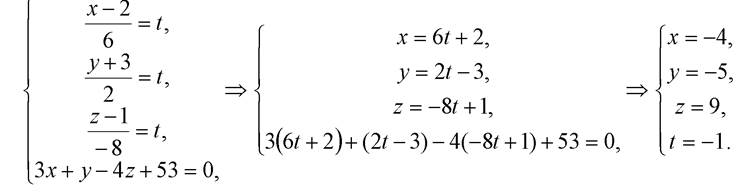
Получили, что точка N (–4; –5; 9) является общей для прямой l и плоскости α, следовательно, 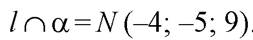
г) В этом случае 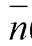 ={-1; 2; 1},
={-1; 2; 1}, 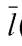 ={7; 3; 5}, M 0(–1; 7; –1). Так как
={7; 3; 5}, M 0(–1; 7; –1). Так как 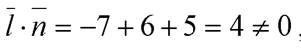 , то прямая l не может ни лежать в плоскости α, ни быть ей параллельной. Координаты
, то прямая l не может ни лежать в плоскости α, ни быть ей параллельной. Координаты 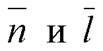 не пропорциональны:
не пропорциональны: 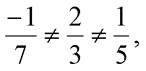
то есть прямая l не перпендикулярна плоскости α. Так как исчерпаны все другие возможности, то остается только один вариант – прямая l и плоскость α пересекаются. Найдем точку их пересечения, решив совместно уравнения: 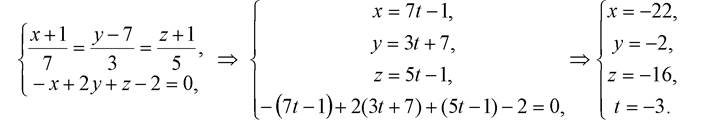
Получили, что точка 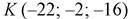 является общей для прямой
является общей для прямой  иплоскости
иплоскости  следовательно,
следовательно, 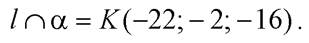
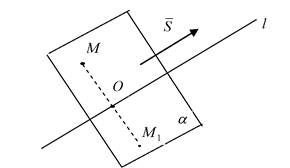
Пример2. Найти точку 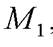 симметричную точке
симметричную точке
M (1,0,- 2) относительно прямой 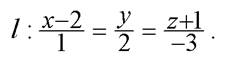
Решение. Сначала составим уравнение плоскости 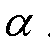 , проходящей через точку M перпендикулярно прямой
, проходящей через точку M перпендикулярно прямой 
Вектор нормали 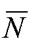 к плоскости
к плоскости  совпадает с направляющим вектором
совпадает с направляющим вектором 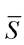 прямой
прямой 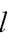 —
— 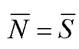 = {1,2,- 3}. Тогда уравнение плоскости имеет вид:
= {1,2,- 3}. Тогда уравнение плоскости имеет вид: 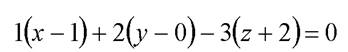 или
или 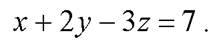 Найдем координаты точки
Найдем координаты точки 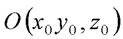 пересечения прямой
пересечения прямой 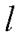 и плоскости
и плоскости 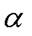 так, как мы это делали в задаче 1. Запишем параметрические уравнения прямой
так, как мы это делали в задаче 1. Запишем параметрические уравнения прямой 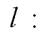
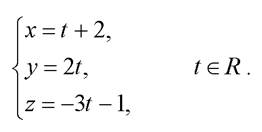
Подставим эти выражения в уравнение плоскости и найдем соответствующее значение параметра 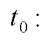
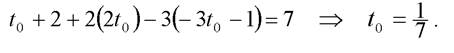
Итак, точка O имеет координаты 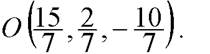
Поскольку точка O является серединой отрезка 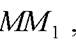
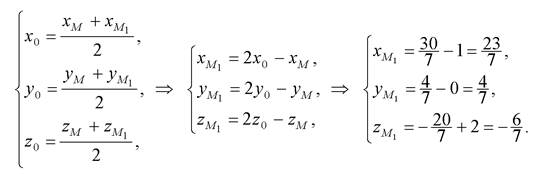
Ответ: точка 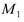 имеет координаты
имеет координаты 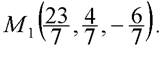
 2015-06-28
2015-06-28 892
892







