Возможны три случая взаимного расположения прямой и плоскости:
- прямая и плоскость пересекаются, т.е. имеют одну общую точку;
- прямая и плоскость параллельны, т.е. не имеют общих точек;
- прямая лежит в плоскости, т.е. все точки прямой принадлежат плоскости.
Получим признаки для всех этих случаев. Пусть прямая 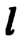 и плоскость
и плоскость 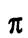 заданы уравнениями:
заданы уравнениями:

т.е. прямая 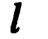 проходит через точку
проходит через точку 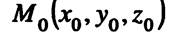 коллинеарно вектору
коллинеарно вектору 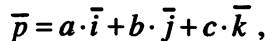 а плоскость
а плоскость 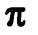 перпендикулярна вектору
перпендикулярна вектору 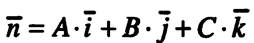
Перечисленным выше случаям взаимного расположения прямой 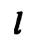 и плоскости
и плоскости 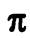 соответствуют следующие признаки:
соответствуют следующие признаки:
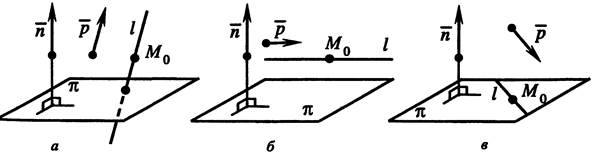
прямая 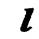 и плоскость
и плоскость 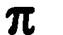 пересекаются
пересекаются  векторы
векторы 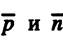 не ортогональны,а);
не ортогональны,а);
- прямая 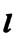 и плоскость
и плоскость 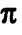 параллельны
параллельны  векторы
векторы 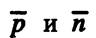 ортогональны, а точка
ортогональны, а точка 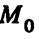 не принадлежит плоскости
не принадлежит плоскости  (рис.б);
(рис.б);
- прямая 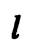 лежит в плоскости
лежит в плоскости 
 векторы
векторы 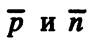 ортогональны, а точка
ортогональны, а точка 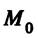 принадлежит плоскости
принадлежит плоскости 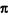 (рис.,в).
(рис.,в).
* 
Учитывая свойство скалярного произведения векторов 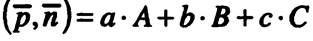 , получаем:
, получаем:
- прямая 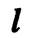 и плоскость
и плоскость 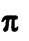 пересекаются
пересекаются 
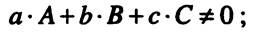
- прямая 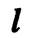 и плоскость '
и плоскость ' 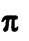 параллельны
параллельны 
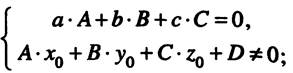
- прямая 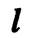 лежит в плоскости
лежит в плоскости 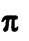

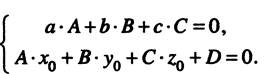
Для того чтобы найти точку пересечения прямой 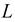
с плоскостью 
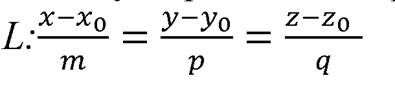
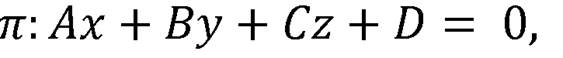 нужно решить систему уравнений прямой и плоскости, предварительно записав уравнения прямой в параметрическом виде:
нужно решить систему уравнений прямой и плоскости, предварительно записав уравнения прямой в параметрическом виде:
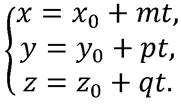
Подставив эти выражения для  в уравнение плоскости и преобразовав его, получим уравнение:
в уравнение плоскости и преобразовав его, получим уравнение: 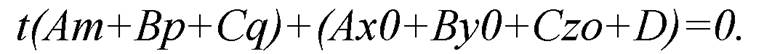 Если прямая
Если прямая 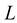 не параллельна плоскости
не параллельна плоскости 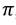 , т. е. если
, т. е. если 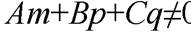 , то из равенства находим
, то из равенства находим 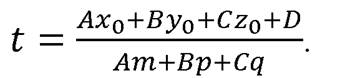
Подставив найденное значение 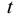 в параметрические уравнения прямой, найдём координаты точки пресечения прямой и плоскости.
в параметрические уравнения прямой, найдём координаты точки пресечения прямой и плоскости.
Рассмотрим случай, когда 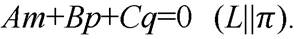 Тогда возможны следующие два случая:
Тогда возможны следующие два случая: 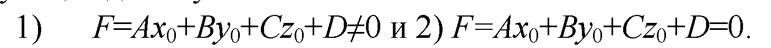
В случае 1) прямая 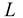 параллельна плоскости
параллельна плоскости 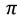 и не пересекает плоскость, т. е. уравнение решения не имеет (так как имеет вид Ot+k=0, к≠О). В случае 2) уравнение имеет вид
и не пересекает плоскость, т. е. уравнение решения не имеет (так как имеет вид Ot+k=0, к≠О). В случае 2) уравнение имеет вид 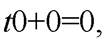 которому
которому
удовлетворяет любое значение 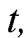 и поэтому любая точка прямой является точкой пересечения прямой и плоскости. Следовательно, прямая L лежит на плоскости
и поэтому любая точка прямой является точкой пересечения прямой и плоскости. Следовательно, прямая L лежит на плоскости 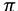 . Таким образом, условие принадлежности прямой плоскости имеет вид
. Таким образом, условие принадлежности прямой плоскости имеет вид
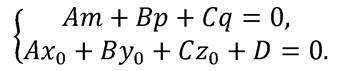
 2015-06-28
2015-06-28 412
412







