Общее уравнение плоскости

Краткое содержание лекций

Векторное и нормальное уравнение плоскости

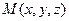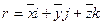Пусть в пространстве задана система прямоугольных декартовых координат Oxyz и некоторая плоскость Р₁ Возьмем произвольную точку , где , и 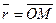- радиус-вектор. Проекция радиус-вектора на направление вектора 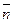пр_n .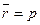

Из свойства скалярного произведения имеем 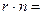пр_n 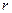, поэтому 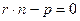(1)

Обозначим через 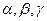углы, образованные единичным вектором 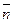с ортами 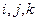. Тогда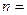

Кроме того, известно, что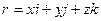

И из (1) формулы, получим (2)

(2) – нормальное уравнение плоскости в координатной форме.

Общее уравнение плоскости.

Уравнение любой плоскости приводится к виду 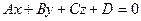(3) где

Коэффициенты 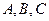является координатами вектора 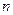, перпендикулярного к плоскости, заданной уравнением. Он называется нормальным вектором этой плоскости и определяет ориентацию плоскости в пространстве относительно системы координат.

Рассмотрим, в чем заключается особенность расположения плоскости, заданной общим уравнением 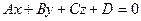, если некоторые коэффициенты этого уравнения обращаются в нуль.