Различные виды уравнения плоскости

1) Пусть в уравнении плоскости 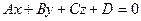все коэффициенты отличны от нуля.

Перенесем в уравнении член 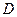в правую часть

равенства и разделим левую и правую часть полученного

уравнения на - :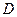

эта форма уравнения плоскости называется уравнением плоскости в отрезках

2) Пусть заданы точки 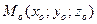и вектор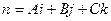

Найдем уравнение плоскости, проходящей через точку 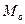и перпендикулярной к вектору 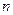. Поскольку вектор 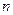задан, то уравнение плоскости, очевидно, будет иметь вид (*)

где остается определить 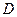из условия, что точка 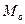лежит в плоскости: (**)

вычитая почленно (**) из (*)

3) Уравнение плоскости по трем точкам. Если плоскость проходит через точки 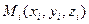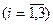не лежащие на одной прямой, то ее уравнение можно записать в виде