2015-06-28
9201. Дан вектор 
. Построить заданный вектор и найти его модуль.
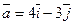
2. Найти координаты вектора 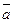, если известно, что он направлен в противоположную сторону к вектору 
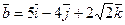, и его модуль равен 5.
3. Даны координаты точек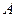 
и 
: 
, 
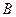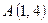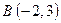. Найти координаты точки 
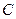, которая делит отрезок 
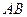в отношении 2: 3.
4. Даны два вектора 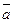и 
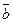. Найти косинус угла между векторами.
, 
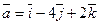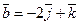
5. Векторы 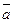и 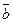составляют угол 450. Найти площадь треугольника, построенного на векторах
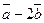и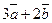 
, если 
.
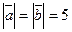6. Дано: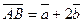 
, 
, 
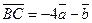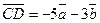. Доказать, что ABCD – трапеция.
7. В точках пересечения прямой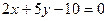 
с осями координат восстановлены перпендикуляры к этой прямой. Найти их уравнения.
8. Найти уравнения прямых, проходящих через точку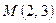 
, под углом 450 к прямой 
.
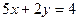9. В треугольнике с вершинами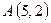 
, 
, 
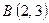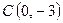найти уравнения медианы и биссектрисы, опущенных из вершины 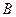, и длину высоты 
.
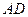10. Даны вершины треугольника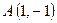 
, 
, 
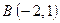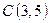. Составить уравнение перпендикуляра, опущенного из вершины 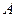на медиану, проведённую из вершины .
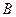11. Даны две точки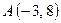 
, 
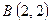. На оси 
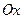найти такую точку 
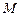, чтобы ломаная 
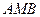имела наименьшую длину.
