2015-06-28
612
Прежде, чем приступить к решению задачи, необходимо ознакомиться с теоретическими основами теплообмена при течении жидкости в трубе [1, стр.78-93]. Следует обратить особое внимание на решение соответствующих задач: [1, стр.92, пример 3-2] и [2, стр.82-83, задача 5-29].
Рекомендуемая последовательность решения задачи:
1. Определить теплофизические свойства масла при его средней температуре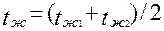 
Для этого достаточно использовать линейную интерполяцию в узлах таблицы 2 или таблицы 3.
Так, например, для масла МС-20 при его средней температуре 87°С, число Прандтля будет равно
,
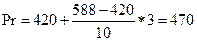где 420 – это значение числа Прандтля при 90°С, 588 – число Прандтля при 80°С.
Аналогично определяются и все остальные теплофизические свойства масла:
плотность, теплоемкость, коэффициент теплопроводности, кинематический коэффициент вязкости.
2. Определить скорость течения масла в трубке
,
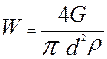где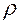 
- плотность масла.
3. Вычислить критерий Рейнольдса
,
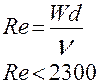где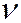 
- кинематический коэффициент вязкости масла.
4. Вычислить критерий Нуссельта (безразмерный коэффициент теплоотдачи)
|
|
|
Если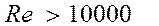 
, то
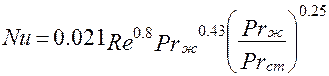(1),
При условии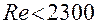 
, число Нуссельта можно принять
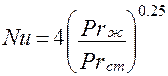(2).
Надежной методики вычисления коэффициент теплоотдачи при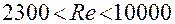 
не существует, но условно можно принять его величину, равной среднему значению между (1) и (2).
В формулах (1) и (2)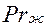 
- число Прандтля жидкости при средней температуре 
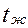, а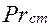 
- число Прандтля жидкости при температуре стенки 
.
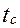5. Вычислить величину физического коэффициента теплоотдачи
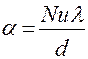
6. Вычислить величину среднего температурного напора по формулам
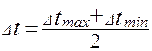в случае 
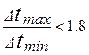или
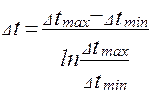при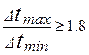 
,
где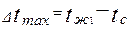 
и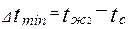 
7. Вычислить плотность теплового потока
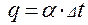
8. Вычислить потребную для нагрева масла мощность теплового потока
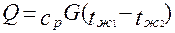
9. Величина поверхности теплообмена определяется как
,
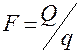а потребная длина трубки
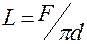
Рекомендуемая литература
1. Михеев М.А., Михеева И.М. Основы теплопередачи. - М.: Энергия, 1977. 344с.
2. Краснощеков Е.А., Сукомел А.С. Задачник по теплопередаче. - М.: Энергия, 1975. 280с.
3. Исаченко В.Н., Осипова В.М., Сукомел А.С. Теплопередача. М., 1981. 488с.
