2.1 Написать уравнение плоскости, проходящей через точку М1 (2; 4; -3) и отсекающей на осях Ох, Оу и Оz отрезки, длины которых находятся в соотношении 2:3:5 соответственно.
Решение:
Пусть 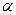 - искомая плоскость, и пусть от оси Ох
- искомая плоскость, и пусть от оси Ох 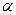 отсекает отрезок, равный 2а. Тогда от оси Оу
отсекает отрезок, равный 2а. Тогда от оси Оу 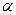 будет отсекать отрезок 3а, а от оси Oz – отрезок, равный 5а. Составим уравнение плоскости
будет отсекать отрезок 3а, а от оси Oz – отрезок, равный 5а. Составим уравнение плоскости 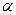 с помощью формулы (8):
с помощью формулы (8):
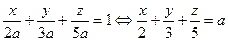 .
.
Найдём значение а, подставив координаты точки М в полученное уравнение:
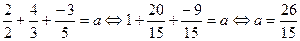 .
.
Тогда уравнение 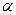 запишем в виде:
запишем в виде:
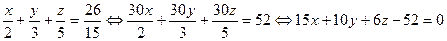 -искомое уравнение.
-искомое уравнение.
Ответ: 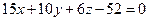 .
.
2.2 Уравнение прямой 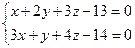 записать в каноническом виде.
записать в каноническом виде.
Построить прямую.
Решение:
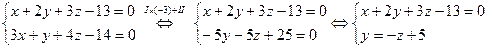
 (Из второго уравнения исключаем х). Получили зависимость у = у (z). Теперь найдём зависимость у = у(х), исключая z:
(Из второго уравнения исключаем х). Получили зависимость у = у (z). Теперь найдём зависимость у = у(х), исключая z:
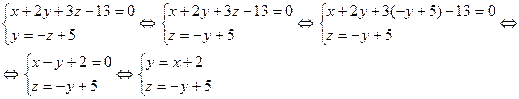
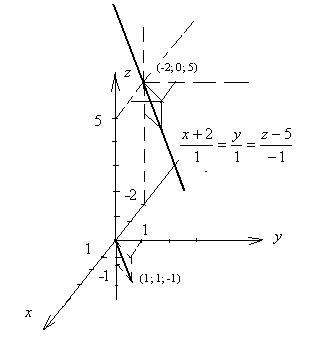
Получили: 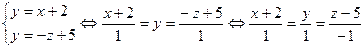 - каноническое уравнение прямой (формула (16)). Прямая проходит через точку с координатами (-2; 0; 5), параллельно вектору (1; 1; -1). Прямая изображена на рисунке 5.
- каноническое уравнение прямой (формула (16)). Прямая проходит через точку с координатами (-2; 0; 5), параллельно вектору (1; 1; -1). Прямая изображена на рисунке 5.
Ответ: 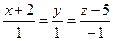 . Рисунок 10.
. Рисунок 10.
3.3 Найти угол прямой 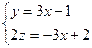 с плоскостью 2х + у + z - 4 = 0.
с плоскостью 2х + у + z - 4 = 0.
Решение:
Найдём каноническое уравнение прямой:
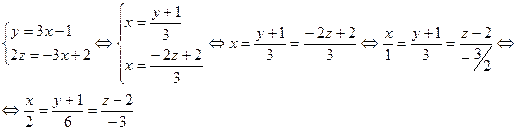
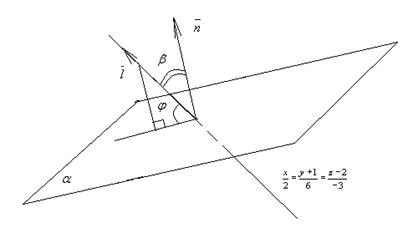 Получили, что прямая, заданная в условии системой двух уравнений, параллельна вектору
Получили, что прямая, заданная в условии системой двух уравнений, параллельна вектору 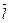 (2; 6; -3). Пусть уравнение 2х + у + z - 4 = 0 задаёт плоскость
(2; 6; -3). Пусть уравнение 2х + у + z - 4 = 0 задаёт плоскость 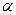 . Тогда угол
. Тогда угол 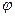 между прямой и плоскостью будет равен углу
между прямой и плоскостью будет равен углу 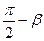 , где
, где 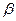 - угол между прямой и нормалью к плоскости
- угол между прямой и нормалью к плоскости 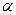 (рисунок 6).
(рисунок 6).
Рисунок 11.
Из 1.2.2 следует, что 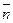 = (2; 1; 1) - вектор нормали к плоскости
= (2; 1; 1) - вектор нормали к плоскости 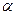 .
.
С помощью формулы (4) найдём угол между векторами 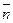 и
и 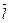 (он и будет равен углу
(он и будет равен углу 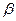 ):
):
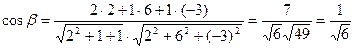
Тогда 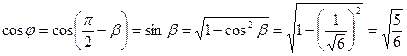 .
.
Ответ: 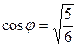
2.4 Найти центр и радиус сферы 1). x2 + y2 +z2 -3x +5y – 4z = 0
2). x2 + y2 +z2 = 2 az. Построить изображение сфер.
Решение:
1). x2 + y2 +z2 -3x +5y – 4z = 0 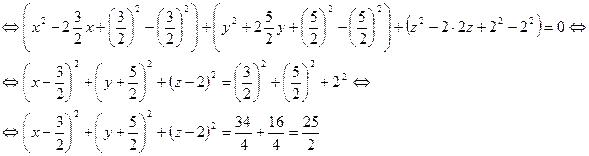
Получили уравнение сферы с центром в точке S 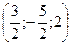 и радиусом
и радиусом
R = 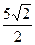 - рисунок 7.
- рисунок 7.
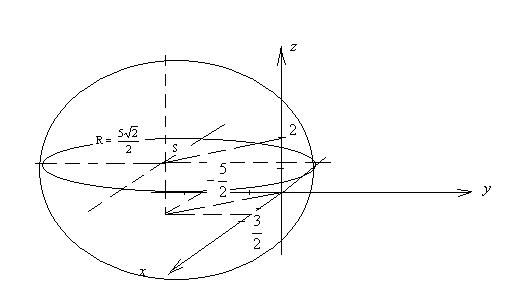
Рисунок 12.
2). x2 + y2 +z2 = 2 az 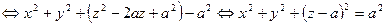 - уравнение сферы с центром в точке (0; 0; а) и радиусом R = a – рисунок 13.
- уравнение сферы с центром в точке (0; 0; а) и радиусом R = a – рисунок 13.
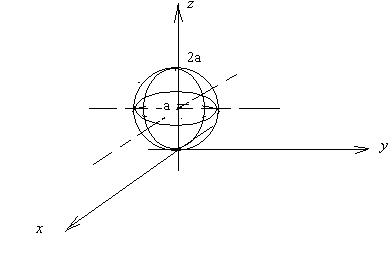
Рисунок 8.
Рисунок 13.
Ответ: 1). Сфера имеет центр в точке S 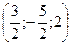 и радиус R =
и радиус R = 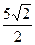 ; 2). Сфера имеет центр в точке (0; 0; а) и радиус R = a.
; 2). Сфера имеет центр в точке (0; 0; а) и радиус R = a.
2.6 Написать уравнение поверхности, образованной вращением эллипса 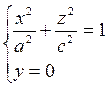 вокруг оси Oz.
вокруг оси Oz.
Решение:
В плоскости у = 0 сечением поверхности является эллипс с полуосями: а и с. Вращая его вокруг оси Oz, получаем поверхность, сечение которой плоскостью x = 0 – так же эллипс. Т.к. при вращении точка с координатами (а; 0; 0) переходит в точку с координатами (0; а; 0), а точка с координатами (0; 0; с) остаётся на месте, то уравнение эллипса в сечении плоскостью х = 0 имеет вид:
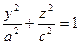 . Т.о. искомая поверхность – эллипсоид вращения с полуосями а, а и с. Следовательно, искомое уравнение можно записать в виде:
. Т.о. искомая поверхность – эллипсоид вращения с полуосями а, а и с. Следовательно, искомое уравнение можно записать в виде: 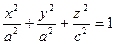 .
.
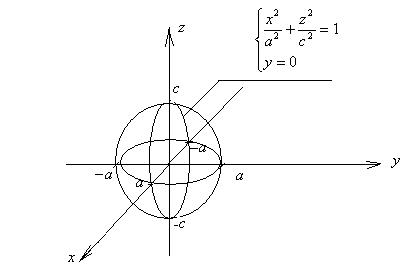
Рисунок 14.
Ответ: 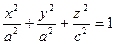 - уравнение эллипсоида вращения.
- уравнение эллипсоида вращения.
2.5 Какому условию должны удовлетворять координаты точки M, если она одинаково удалена от точек А(7; -3) и В(-2; 1)?
Решение:
Пусть точка М имеет координаты (x; y). Найдём координаты векторов 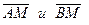 :
:
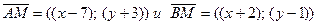 . Из условия имеем: АМ = ВМ, а следовательно,
. Из условия имеем: АМ = ВМ, а следовательно, 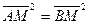 . Запишем квадраты длин отрезков АМ и ВМ, используя свойства скалярного произведения:
. Запишем квадраты длин отрезков АМ и ВМ, используя свойства скалярного произведения:
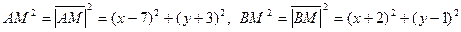
Т.к. квадраты длин равны, получим уравнение:
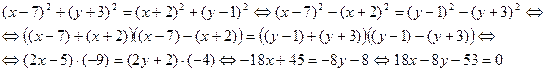 .
.
Получили, что точка М, удовлетворяющая условию задачи, лежит на прямой 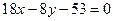 .
.
II способ:
Т.к. точка М равноудалена от А и В, то она находится на серединном перпендикуляре прямой (АВ). Найдём середину отрезка АВ:
Пусть N(х0; у0) середина отрезка АВ, тогда
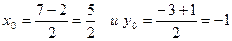 .
.
Будем искать уравнение прямой (MN). Т.к. (MN) 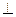 (АВ), угловой коэффициент (MN) найдём из уравнения прямой (АВ). По формуле уравнения прямой, проходящей через две известные точки, для точек А и В получим:
(АВ), угловой коэффициент (MN) найдём из уравнения прямой (АВ). По формуле уравнения прямой, проходящей через две известные точки, для точек А и В получим:
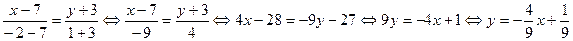
Из последнего уравнения следует, что угловой коэффициент прямой (АВ) равен 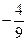 , тогда прямая (MN) имеет угловой коэффициент равный
, тогда прямая (MN) имеет угловой коэффициент равный 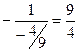 . Тогда уравнение (MN) можно записать в виде:
. Тогда уравнение (MN) можно записать в виде: 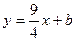 . Свободный член
. Свободный член 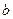 получим, подставив в уравнение (MN) координаты точки N
получим, подставив в уравнение (MN) координаты точки N 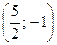 :
:
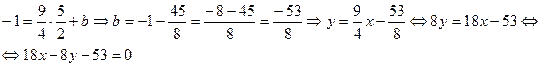
Последнее уравнение – уравнение прямой (MN) – выражает условие, при котором точка M будет равноудалена от точек А и В.
Ответ: 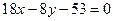 .
.
2.6 Даны точки М1 (-1, -2, 0) и М2 (1, 1, 2). Написать уравнение плоскости, проходящей через М1 и М2 и перпендикулярной к плоскости х + 2у + 2z – 4 = 0.
Решение:
Пусть 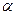 - искомая плоскость, задаваемая уравнением Ах + Ву + Сz + D = 0. Вектор (А,В,С) - вектор нормали к плоскости
- искомая плоскость, задаваемая уравнением Ах + Ву + Сz + D = 0. Вектор (А,В,С) - вектор нормали к плоскости 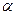 :
: 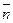 = (А,В,С).
= (А,В,С).
Пусть уравнение х + 2у + 2z – 4 = 0 задаёт плоскость 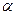 1, вектор нормали которой
1, вектор нормали которой 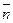 1 будет иметь координаты (1; 2; 2). Т.к. плоскости перпендикулярны,
1 будет иметь координаты (1; 2; 2). Т.к. плоскости перпендикулярны, 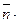
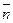 1= 0. Тогда по свойству скалярного произведения векторов получим уравнение: А + 2В + 2С = 0. Ещё два уравнения получим, подставив координаты точек М1 и М2 в уравнение плоскости
1= 0. Тогда по свойству скалярного произведения векторов получим уравнение: А + 2В + 2С = 0. Ещё два уравнения получим, подставив координаты точек М1 и М2 в уравнение плоскости 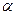 :
:
-А – 2В + С + D = 0 и А + В + 2С + D = 0.
Составим систему линейных уравнений:
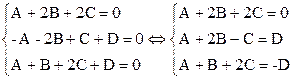 . Система содержит три уравнения и четыре неизвестных, следовательно, одну переменную можно считать свободной, например D, и выражать через неё остальные. Составим расширенную матрицу системы и с помощью метода Гаусса (1.3) получим её решение:
. Система содержит три уравнения и четыре неизвестных, следовательно, одну переменную можно считать свободной, например D, и выражать через неё остальные. Составим расширенную матрицу системы и с помощью метода Гаусса (1.3) получим её решение:
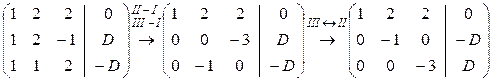
Из последнего уравнения следует: 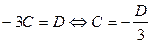 , из второго уравнения получим, что В = D. Из первого выражаем А:
, из второго уравнения получим, что В = D. Из первого выражаем А:
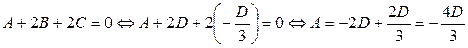
Тогда искомое уравнение плоскости  можно записать в виде:
можно записать в виде:
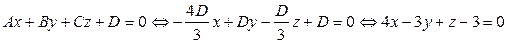
Ответ: 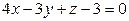 .
.
2.7 Эллипс, симметричный относительно осей координат, фокусы которого находятся на оси Ох, проходит через точку М (-4; 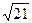 ) и имеет эксцентриситет е = ¾. Написать уравнение эллипса и найти фокальные радиус – векторы точки М. Написать уравнения директрис.
) и имеет эксцентриситет е = ¾. Написать уравнение эллипса и найти фокальные радиус – векторы точки М. Написать уравнения директрис.
Решение:
Будем искать уравнение эллипса в виде: 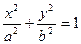 .
.
a и b найдём, подставив в уравнение эллипса координаты точки М: 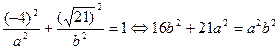 .
.
Т.к. 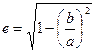 , получим второе уравнение:
, получим второе уравнение: 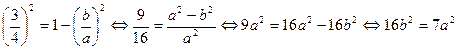 .
.
Решим систему двух уравнений с двумя неизвестными:
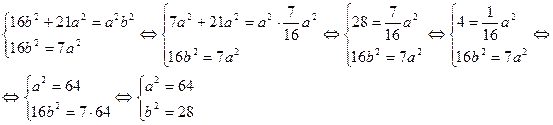
Тогда искомым уравнением эллипса будет уравнение: 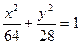 , при этом а = 8, b=
, при этом а = 8, b= 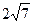 .
.
По формулам для радиус-векторов точки М получим:
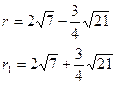
Уравнения директрис при а = 8 можно записать в виде:
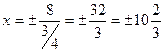
Ответ: 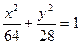 ,
, 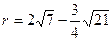 ,
, 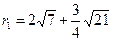 , уравнения директрис:
, уравнения директрис: 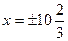 .
.
2.8 Написать уравнение гиперболы, симметричной относительно осей координат, проходящей через точку (2р, р 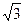 ), у которой е =
), у которой е = 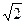 . Найти уравнения асимптот и директрис.
. Найти уравнения асимптот и директрис.
Решение:
Будем искать уравнение гиперболы в виде: 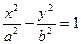 .
.
Параметры a и b найдём, подставив в уравнение гиперболы координаты точки (2р, р 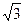 ):
): 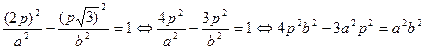 .
.
Т.к. 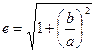 , получим второе уравнение:
, получим второе уравнение: 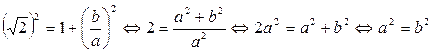 .
.
Решим систему двух уравнений с двумя неизвестными:
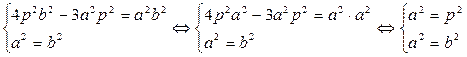
Тогда искомым уравнением гиперболы будет уравнение: 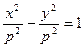 , при этом, а=b=p.
, при этом, а=b=p.
Асимптоты гиперболы можно записать в виде: 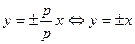 . Т.о. асимптотами гиперболы являются биссектрисы координатных углов. Директрисами гиперболы являются прямые х =
. Т.о. асимптотами гиперболы являются биссектрисы координатных углов. Директрисами гиперболы являются прямые х = 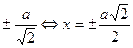 .
.
 2015-06-28
2015-06-28 8659
8659








