Плоскость и прямая в пространстве

1.2.1 Всякое уравнение I степени относительно x,y,z является уравнением плоскости:

Ах + Ву + Сz + D = 0 – общее уравнение плоскости (5)

Рассмотрим точки .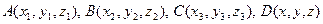

Из компланарности соответствующих векторов получим:

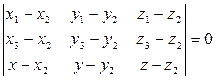(6)

(6) – уравнение плоскости, проходящей через три данные точки.

По свойствам определителя из (6) можно получить второе уравнение плоскости по координатам трёх данных точек:

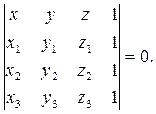(7)

Если в уравнении (5) D = 0, то плоскость проходит через начало координат. Плоскость Ву + Сz + D = 0 (А = 0) параллельна Ох. Аналогично при В = 0 и С = 0 получим плоскости, параллельные Оу и Оz соответственно.

Пусть А = 0 и В = 0. Тогда из (5) следует Сz + D = 0 или 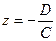- плоскость, параллельная плоскости z = 0.

Уравнение плоскости, отсекающей от координатных осей соответствующие отрезки: 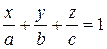(8)

Нормальное уравнение плоскости:

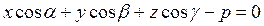(9)

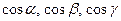- направляющие косинусы перпендикуляра, опущенного из начала координат на плоскость (т.е. косинусы углов между этим перпендикуляром и положительными направлениями соответствующих осей координат). р – длина перпендикуляра.

Общее уравнение плоскости (5) можно привести к виду (9), умножив его на нормирующий множитель М:

М = 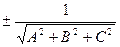(10)

Расстояние от любой точки К 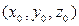пространства до плоскости можно вычислить по формулам:

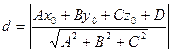(11)

или 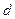= 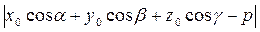(12)

1.2.2 Угол между двумя плоскостями

Рассмотрим плоскость 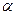, заданную уравнением (4). Вектор (А,В,С) называется вектором нормали к плоскости 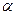: 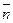= (А,В,С). Тогда угол между двумя плоскостям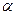и и 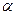₁, заданной уравнением А₁х + В₁у + С₁z + D₁ = 0, будет равен углу между их нормалями 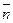и ₁:

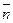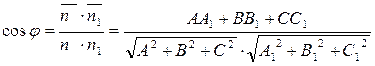(13)

Тогда, если плоскости перпендикулярны, то 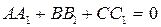, если плоскости параллельны, то координаты их нормалей должны быть пропорциональны: .

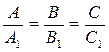1.2.3 Прямая в пространстве

Пусть Ах + Ву + Сz + D = 0 – уравнение плоскости 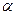, а А₁х + В₁у + С₁z + D₁ = 0 – уравнение плоскости 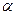₁. Если плоскости не являются параллельными, то система этих двух уравнений задаёт прямую l - линию пересечения 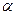и 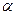₁,. Следовательно, прямую можно задать системой:

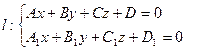(14)

Рассмотрим точки 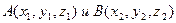. Из коллинеарности векторов 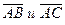, где С(х, у, z) - произвольная точка прямой (АВ), аналогично уравнению прямой на плоскости получим

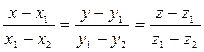(15)

(15) - уравнение прямой, проходящей через две заданные точки. Из него следует каноническое уравнение прямой:

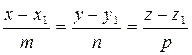(16)

Здесь 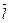(m, n, p) – вектор, параллельный прямой l, 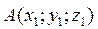лежит на прямой.

Пусть известны канонические уравнения прямых, параллельных векторам соответственно 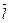(m, n, p) и 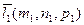. Тогда угол между прямыми можно определить, как угол между векторами :

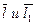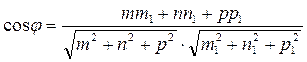(17)

Если 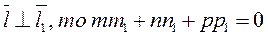(18)

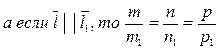. (19)

Может оказаться, что координаты вектора 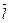(m, n, p) - нулевые, тогда в записи уравнения (16) допускаются нули в знаменателе. Так, например, если m = 0, то получим из первого равенства уравнения (15), что n(x-x₁)=0(y-y₁)=0, т.е. получим, что x = x₁ для любых точек прямой. Следовательно, прямая перпендикулярна Ох. (Аналогично для n = 0: 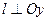и для р = 0: 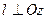). Если m = 0, и n = 0, то прямая параллельна Оz и т.д.

Пусть прямые l и l ₁ заданы уравнениями: 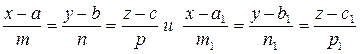соответственно. Тогда необходимым и достаточным условием пересечения прямых будет условие:

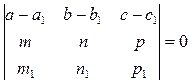
(20)

Здесь .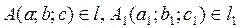

Тогда уравнение плоскости, проходящей через точку А₁, параллельно векторам :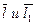

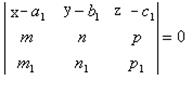
(21)