Пусть 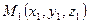 ,
,  ,
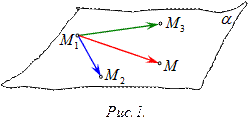
, 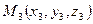 три точки, не лежащие на одной прямой и принадлежащие плоскости
три точки, не лежащие на одной прямой и принадлежащие плоскости  (рис.1). Возьмем произвольную точку
(рис.1). Возьмем произвольную точку 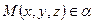 , тогда вектора
, тогда вектора
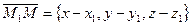 ,
,
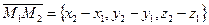 ,
,
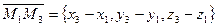 ‑
‑
компланарные, т.е.
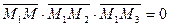 (1)
(1)
Уравнение (1) – это уравнение плоскости, проходящей через три точки. Запишем это уравнение в координатной форме:
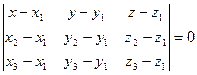 (2)
(2)
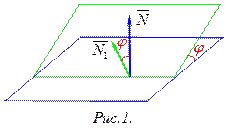
Взаимное расположение двух плоскостей.
Даны две плоскости 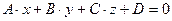 и
и 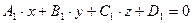 , с соответствующими направляющими векторами
, с соответствующими направляющими векторами 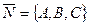 и
и 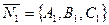 . Если
. Если 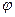 ‑ двугранный угол между этими плоскостями, то он равен углу, образованному векторами
‑ двугранный угол между этими плоскостями, то он равен углу, образованному векторами 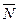 и
и 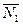 .
.
Таким образом, имеем
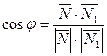 ,
,
где 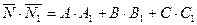 ,
, 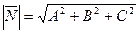 ,
, 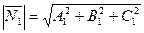 .
.
Отсюда получаем:
условие параллельность плоскостей
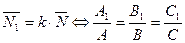 ;
;
условие перпендикулярности плоскостей
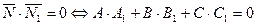 .
.
 2015-06-28
2015-06-28 241
241








