Теплообмена

Основной целью решения задач конвективного теплообмена является определение поля температур (энтальпий), скоростей и вектора плотности теплового потока. Для этого необходимо иметь соответствующие уравнения энергии, движения, сплошности, а также условия однозначности, описывающие все частные особенности рассматриваемой задачи.

1.2.1. Уравнения неразрывности

Известно, что масса изолированной системы m во всё время движения остаётся неизменной (закон сохранения массы), т.е.

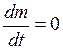, (1.30)

где t – время.

Для конечного постоянного объёма среды τ, ограниченного неподвижной замкнутой поверхностью произвольной формы σ («контрольной поверхностью») изменение массы

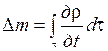, (1.31)

где 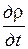- изменение плотности среды в единицу времени в единице объёма.

Иначе величину 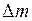можно определить как разность количества среды (жидкости), вытекающей из объёма и втекающей в него:

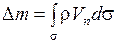, (1.32)

где 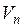- проекция вектора скорости 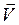на нормаль к площадке .

Положительному значению интеграла по поверхности соответствует вытекание из объёма некоторого количества жидкости, при уменьшении массы плотность жидкости будет убывать и интеграл по объёму (1.31) примет отрицательное значение.

По формуле Остроградского-Гаусса

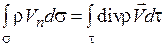. (1.33)

Поэтому

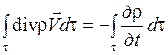. (1.34)

Уравнение (1.34) можно записать и следующим образом:

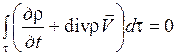. (1.35)

Интеграл по произвольному объёму будет равен нулю в случае, если подынтегральная непрерывная функция равна нулю.

Поэтому

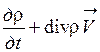(1.36)

Поскольку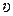

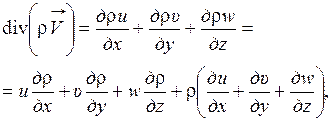
(1.37)

где 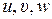- проекции вектора скорости 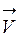на оси (Ox, Oy, Oz) прямоугольных декартовых координат, а

,

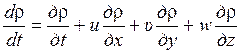уравнение сохранения массы (неразрывности или сплошности) (1.36) можно представить ещё в следующем виде:

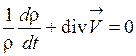. (1.38)

Если жидкость несжимаема (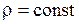), то

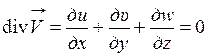(1.39)

и

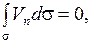(1.40)

т.е. поток скорости через любую замкнутую поверхность равен нулю.

Для стационарного движения уравнение (1.36) примет вид

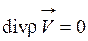(1.41)

или

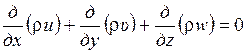(1.42)

Уравнение (1.37) можно представить и в следующем виде

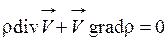. (1.43)

1.2.2 Уравнения движения

Уравнения движения жидкости и газа, как было показано в курсе гидромеханики, могут быть получены из уравнений движения сплошных сред в напряжениях. В проекциях на координатные оси прямоугольной системы координат отнесённые к единице объёма эти уравнения имеют вид

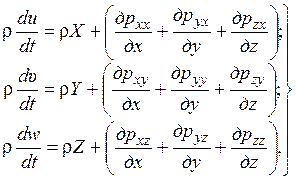(1.48)

где 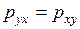, , 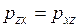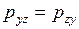- касательные напряжения сил трения или иначе недиагональные компоненты тензора напряжений.

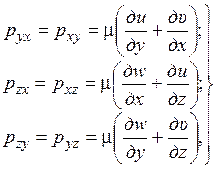(1.49)

где 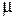- динамический коэффициент вязкости; 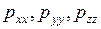- нормальные составляющие напряжений или иначе диагональные компоненты тензора напряжений

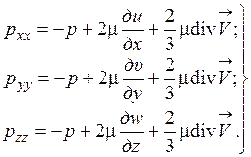(1.50)

Уравнения (1.49) и (1.50) являются формулировкой обобщённого закона Ньютона для связи напряжений и скоростей деформации или соответствующих компонент тензора напряжений и тензора скоростей деформации.

Поскольку вектора напряжений поверхностных сил 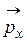, 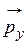и 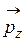, приложенных к площадкам, нормальным осям x, y и z равны

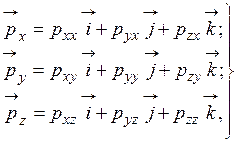(1.51)

то уравнение в напряжениях (1.48) в векторном виде можно представить следующим образом

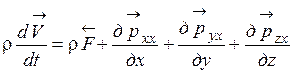. (1.52)

Уравнения движения сжимаемых жидкостей (газов) могу быть получены аналогичным образом.

Подставляем значения компонентов тензора напряжений (1.49), (1.50) в уравнения движения в напряжениях (1.48) в результате после элементарных преобразований получим уравнения движения сжимаемой жидкости (газа)

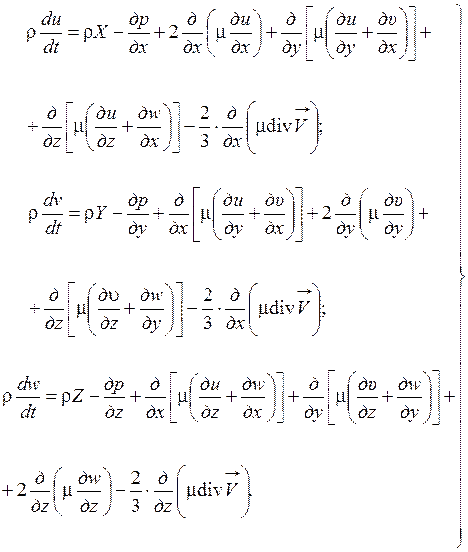(1.53)

Уравнение неразрывности для сжимаемой жидкости (газа) имеет вид

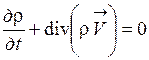(1.54)

или

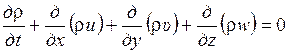(1.55)

Возникающие в вязкой среде силы трения приводят при высоких скоростях движения потока к значительной диссипации энергии в пределах пограничного слоя. Напомним, что под диссипацией энергии (dissipation of energy) понимается преобразование кинетической энергии жидкости в теплоту, обусловленное работой сил вязкости.

Рассмотрим изотермическое движение вязкой несжимаемой жидкости. В этом случае 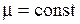, , 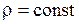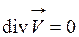. Если в уравнение движения в напряжениях (1.48), представить значения компонентов тензора напряжений, согласно обобщённому закону Ньютона, то для рассматриваемых условий получим следующую систему уравнений в проекциях на оси.

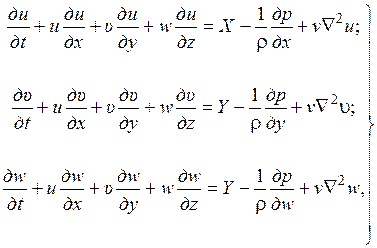(1.58)

К системе (1.58) необходимо присоединить уравнение сплошности или неразрывности

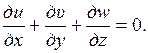(1.59)

Полученные уравнения и являются уравнениями движения изотермической вязкой несжимаемой однородной жидкости, которые называются уравнения Навье-Стокса.

В векторном виде они записываются следующим образом:

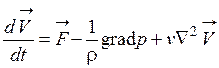; (1.60)

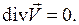(1.61)

Иначе уравнения (1.56) и (1.57) можно представить следующим образом:

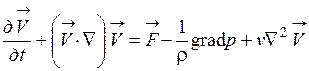; (1.62)

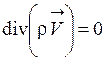. (1.63)

Уравнения (1.60) и (1.62) описывают движение вязкой жидкости при вынужденном и свободном движении жидкости

Рассмотрим случай движения жидкости, когда ее плотность изменяется только в зависимости от температуры. Разность плотностей холодных и нагретых частиц жидкости приведет к появлению свободного движения. Для многих задач конвективного теплообмена, связанных со свободным гравитационным движением, с достаточной для технических расчетов точностью можно ограничиться учетом только возникающих при этом подъемных сил, опуская из рассмотрения силы тяжести. Подъемная (архимедова) сила на единицу объема среды равна 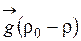, где ρ₀, ρ – плотности, соответствующие температурам Т ₀, Т.

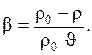(1.64)

Тогда

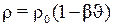; (1.65)

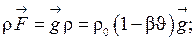(1.66)

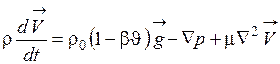. (1.67)

Член уравнения

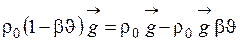, (1.68)

где 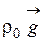– сила тяжести при ρ = ρ₀; 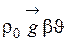– подъемная (архимедова) сила.

Силу тяжести 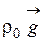можно представить как градиент гидростатического давления p ₀ в покоящейся жидкости с плотностью 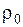. При этом в уравнении (1.63) вместо 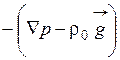можно записать 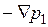, т.е. принять

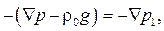(1.69)

где р ₁= р – р ₀.

Если опустить индекс «0» при ρ и индекс «1» при р и разделить все члены полученного уравнения на ρ, то в результате уравнение движения для свободного гравитационного движения можно представить в виде

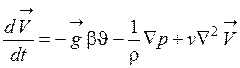. (1.70)

Таким образом уравнения Навье-Стокса для свободного гравитационного движения вязкой несжимаемой жидкости могут быть записаны следующим образом:

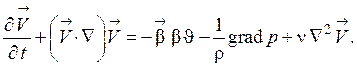(1.71)

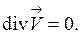(1.72)

В технических устройствах наряду со свободным гравитационным движением на интенсивность конвективного теплообмена часто оказывает влияние свободное движение, вызванное центробежным эффектом или полем центростремительных сил.

Система уравнений, описывающих стационарное течение вязкой несжимаемой жидкости, находящейся под воздействием одновременно гравитационных и центростремительных массовых сил в системе координат, вращающихся с постоянной угловой скоростью ω (такая система координат часто используется для анализа и решения задач течения жидкости во вращающихся трубах), имеет вид

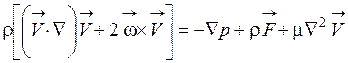; (1.74)

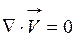. (1.75)

Плотность среды в общем случа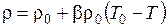е , где 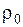- значение плотности при характерной температуре. Уравнения записанные для случая постоянных физических свойств, за исключением изменения плотности, учитываемого в члене массовых сил.

1.2.3 Уравнение энергии

Уравнение сохранения энергии для рассматриваемого объема жидкости τ в гидромеханике записывалось следующим образом:

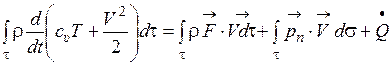, (1.76)

По формуле Остроградского – Гаусса интеграл по поверхности заменяем интегралом по объему:

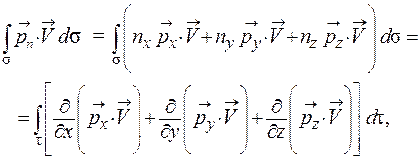(1.77)

где 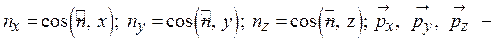векторы напряжений поверхностных сил, приложенных к граням, нормальным соответственно осям Ох, Oy, Oz.

Представляем полученный результат в уравнение (1.76), считая подынтегральную функцию всех интегралов по одному и тому же произвольному объему непрерывной, уравнение сохранения энергии запишем в виде

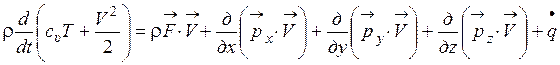, (1.78)

где – результирующее количество теплоты, подводимое в единицу времени к единице объема среды извне и внутренними источниками теплоты: электрическими, химическими и т.п.

Используя уравнение движения сплошной среды в напряжениях, запишем

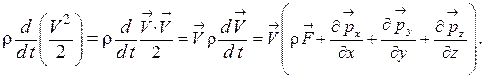(1.79)

Имея в виду, что

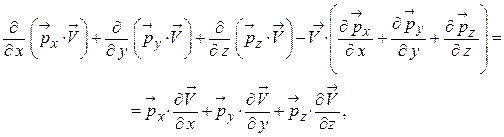
заменяем величину 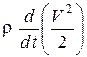в уравнении энергии и после несложных преобразований представляем его в виде

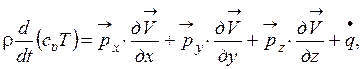(1.80)

где

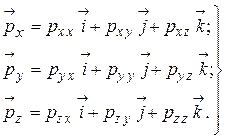(1.81)

Уравнению (1.80) можно придать и другой вид.

Записываем уравнение (1.80) в проекциях на координатные оси, а затем, заменив по обобщенному закону Ньютона компоненты тензора напряжений компонентами тензора скоростей деформаций, представляем уравнение энергии в новом виде

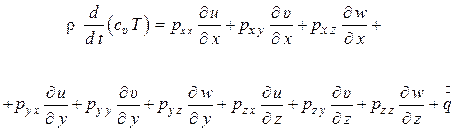(1.82)

или

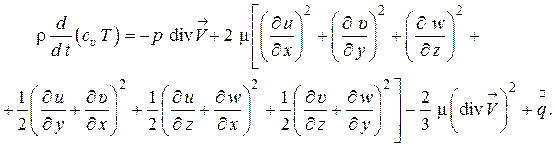
(1.83)

Иначе

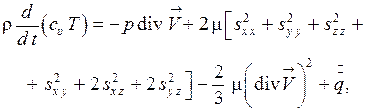(1.84)

где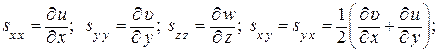

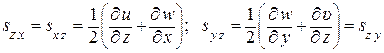– компоненты тензора скоростей деформаций.

Сумма 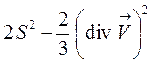носит название диссипативной функции и обозначается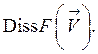

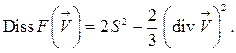(1.85)

Диссипативная функция была введена Рэлеем.

С использованием диссипативной функции, уравнение (1.84) может быть представлено следующим образом:

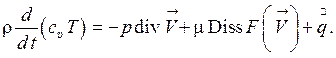(1.86)

Заметим, что произведение 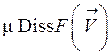– часть мощности внутренних поверхностных сил вязкой жидкости, которая необратимо за счет вязкого трения превращается в теплоту. Этот член в уравнении энергии при большой скорости движения потока и резком изменении ее в пределах пограничного слоя у обтекаемой поверхности может иметь существенное значение.

В соответствии с уравнением сплошности

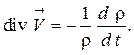(1.87)

Заменив 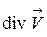по формуле (1.87) и учитывая, что

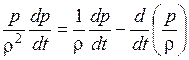, (1.88)

представим уравнение (1.86) в виде

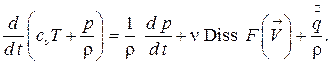(1.89)

Если пренебречь переносом теплоты радиацией (излучением), то подвод теплоты к элементу среды будет определяться только теплопроводностью и внутренними источниками.

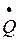= Q_υ – Q _т , (1.91

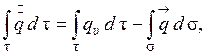(1.92)