Плоскость как поверхность первого порядка

Аналитическая геометрия в пространстве

Теорема. В декартовой прямоугольной системе координат каждая плоскость определяется уравнением первой степени.

Доказательство. Рассмотрим произвольную плоскость П и докажем, что эта плоскость определяется уравнением первой степени. Возьмем на плоскости p какую-нибудь точку

М₀(x₀; y₀; z₀); выберем кроме этого, произвольный вектор (не нулевой) перпендикулярный к плоскости 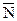П. ^П.

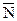={А; В; С}. Пусть М(x; y; z) - произвольная точка. Она лежит на плоскости тогда и только тогда, когда вектор 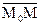перпендикулярен вектору N:

^

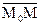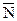
Условием перпендикулярности двух векторов является равенство нулю их скалярного произведения:

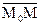={x- x₀; y- y₀; z- z₀}; 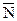={А; В; С}.

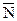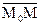× =0 Þ А(x- x₀)+В(y- y₀)+С(z- z₀)=0 (1)

Это и есть искомое уравнение плоскости П, т.к. ему удовлетворяют координаты x; y; z точки М тогда и только тогда, когда М лежит на плоскости П.

Раскрывая скобки, представим уравнение (1) в виде Аx+Вy+Сz+(-Аx₀-Вy₀-Сz₀)=0. Далее, обозначая число -Аx₀-Вy₀-Сz₀ буквой D, получим:

Аx+Вy+Сz+D=0.

Мы видим, что плоскость П действительно определяется уравнением первой степени. Теорема доказана.

Произвольный ненулевой вектор, перпендикулярный плоскости, называется нормальным к ней вектором. Употребляя это название, мы можем сказать, что уравнение А(x- x₀)+В(y- y₀)+С(z- z₀)=0 есть уравнение плоскости, проходящей через точку М₀(x₀; y₀; z₀) и имеющей нормальный вектор N={А; В; С}.

Уравнение вида

Аx+Вy+Сz+D=0 (2)

называется общим уравнением плоскости.

Теорема. В декартовых координатах каждое уравнение первой степени определяет плоскость.

Отметим теперь следующее важное утверждение: если два уравнения А₁x+В₁y+С₁z+D₁=0 и А₂x+В₂y+С₂z+D₂=0 определяют одну и ту же плоскость, то коэффициенты их пропорциональны.