Профиль 9

1.Пло­щадь по­верх­но­сти куба равна 18. Най­ди­те его диа­го­наль.

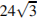2.Объем куба равен . Най­ди­те его диа­го­наль.

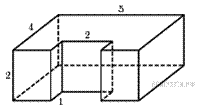
3.Най­ди­те объем мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы пря­мые).

4.В ци­лин­дри­че­ский сосуд на­ли­ли 2000 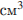воды. Уро­вень воды при этом до­сти­га­ет вы­со­ты 12 см. В жид­кость пол­но­стью по­гру­зи­ли де­таль. При этом уро­вень жид­ко­сти в со­су­де под­нял­ся на 9 см. Чему равен объем де­та­ли? Ответ вы­ра­зи­те в .

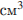5.Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки 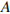, , 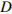, , 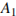, 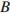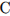пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да 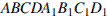, у ко­то­ро­го , , .

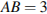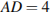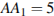6. бак, име­ю­щий форму пра­виль­ной четырёхуголь­ной приз­мы со сто­ро­ной ос­но­ва­ния, рав­ной 20 см, на­ли­та жид­кость. Для того чтобы из­ме­рить объём де­та­ли слож­ной формы, её пол­но­стью по­гру­жа­ют в эту жид­кость. Най­ди­те объём де­та­ли, если уро­вень жид­ко­сти в баке под­нял­ся на 20 см. Ответ дайте в ку­би­че­ских сан­ти­мет­рах.

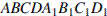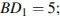
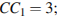
7.В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­но, что 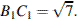Най­ди­те длину ребра .

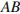8.Через сред­нюю линию ос­но­ва­ния тре­уголь­ной приз­мы, объем ко­то­рой равен 32, про­ве­де­на плос­кость, па­рал­лель­ная бо­ко­во­му ребру. Най­ди­те объем от­се­чен­ной тре­уголь­ной приз­мы.

9.Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки 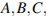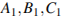пра­виль­ной ше­сти­уголь­ной приз­мы 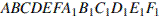, пло­щадь ос­но­ва­ния ко­то­рой равна 6, а бо­ко­вое ребро равно 3.

10.В пра­виль­ной тре­уголь­ной пи­ра­ми­де 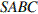ме­ди­а­ны ос­но­ва­ния 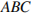пе­ре­се­ка­ют­ся в точке . Пло­щадь тре­уголь­ни­ка равна 2; объем пи­ра­ми­ды равен 6. Най­ди­те длину от­рез­ка .

11.В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де 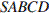точка – центр ос­но­ва­ния, – вер­ши­на, 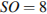, 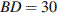. Най­ди­те бо­ко­вое ребро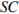

12.Во сколь­ко раз уве­ли­чит­ся объем пра­виль­но­го тет­ра­эд­ра, если все его ребра уве­ли­чить в два раза?

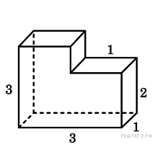13.Най­ди­те квад­рат рас­сто­я­ния между вер­ши­на­м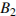и и 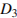мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые.

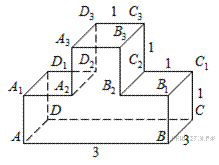
14.Най­ди­те объем мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы мно­го­гран­ни­ка пря­мые).

15.Конус впи­сан в ци­линдр. Объем ко­ну­са равен 5. Най­ди­те объем ци­лин­дра.