Свободные затухающие колебания. Модель свободных затухающих колебаний, согласно рисунку 8, включает демпфер 2, а сила, выводящая из состояния покоя

Модель свободных затухающих колебаний, согласно рисунку 8, включает демпфер 2, а сила, выводящая из состояния покоя, мгновенно приложена к телу и колебания происходят вне воздействия этой силы.

Уравнение имеет вид

,

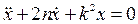где 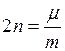; ; 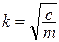m – коэффициент сопротивления.

1. Случай малого сопротивления n < k

Общее решение дифференциального уравнения

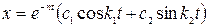
или в ином виде

,

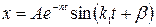где частота затухающих колебаний

.

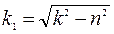Постоянные интегрирования определяются из начальных условий при , , :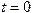

; .

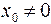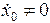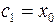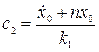Амплитуда колебаний и фаза колебаний определяются следующим образом:

, .

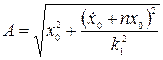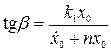Период затухающих колебаний .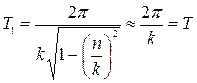

Декремент затухания

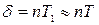, где .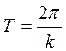

2. Предельный случай n = k

Решение имеет вид .

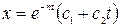Постоянные интегрирования определяем из начальных условий при , , :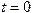

; .

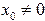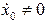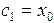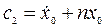При 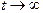x становится неопределенностью типа 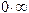. По правилу Лопиталя 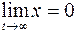материальная точка совершает апериодическое затухающее движение.

3. Случай большого сопротивления n > k

Общее решение дифференциального уравнения имеет вид

.

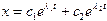Постоянные интегрирования определяем из начальных условий при , , :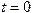

; ,

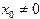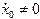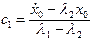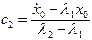где ; .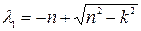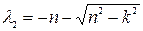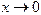

При при 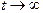имеет место апериодическое затухающее движение.

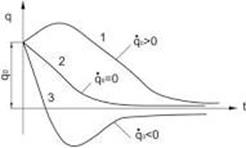
Рис.4. Апериодическое движение